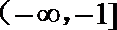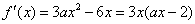- 导数的应用
- 共1166题
21.已知函数

(1)求函数

(2)若存在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若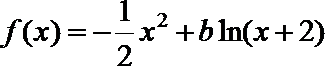
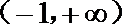
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
21. 已知:函数



(1)求:
(2)求:
正确答案
(Ⅰ)由题意得
因此
因为函数

即对任意实数x,有
从而3a+1=0,b=0,解得
因此

(Ⅱ)由(Ⅰ)知

令


当


从而


当



由前面讨论知,

而


因此


解析
解析已在路上飞奔,马上就到!
知识点
21.已知平面向量a=(

(1)证明a⊥b;
(2)若存在不同时为零的实数k和t,使x=a+ (t2–3)b,y=–ka+tb,且x⊥y,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况。
正确答案
(1)证明:∵a·b=
(2)解:∵x⊥y,∴x·y=0
即[a+(t2–3)b]·(–ka+tb)=0,整理后得
–ka2+[t–k(t2–3)]a·b+t(t2–3)·b2=0
∵a·b=0,a2=4,b2=1
∴上式化为–4k+t(t2–3)=0,∴k=
(3)解:讨论方程

于是f′(t)=

令f′(t)=0,解得t1=–1,t2=1.当t变化时,f′(t),f(t)的变化情况如下表:
当t=–1时,f(t)有极大值,f(t)极大值=
当t=1时,f(t)有极小值,f(t)极小值=–
而f(t)=


所以f(t)的图象大致如下:
于是当k>

当k=



解析
解析已在路上飞奔,马上就到!
知识点
17.已知:定义在R上的函数
(1)若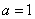
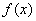
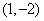
(2)若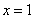
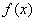
(3)若函数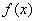

正确答案
解:(1)当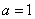
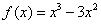
则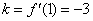
∴切线方程: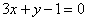
(2)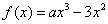
∵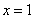
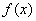
∴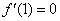
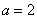
(3)①当a=0时,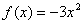
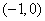
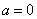
②当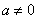
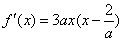
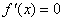
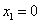
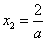
当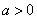
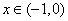
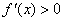
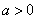
当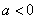
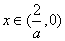

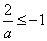

综上所述,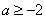
解析
解析已在路上飞奔,马上就到!
知识点
19. 设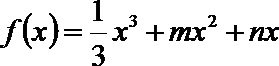
(1)如果
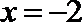
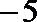
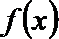
(2)如果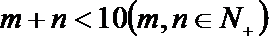
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析