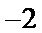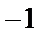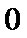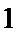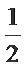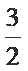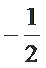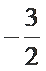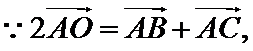- 向量在几何中的应用
- 共120题
15.已知



正确答案
解析
如图所示
∵P,O,Q三点共线,则
∵
∴
∴
考查方向
解题思路
先利用向量的几何意义,利用三点共线,得出
易错点
本题不会利用三点共线转化
知识点
5.在平面直角坐标系中,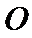
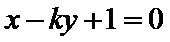
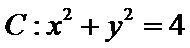
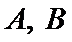
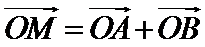
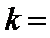
正确答案
解析
设AB中点为D,由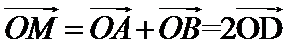
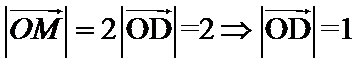
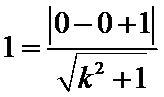
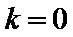
考查方向
解题思路
设AB中点为D,有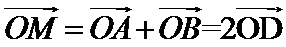
易错点
对已知条件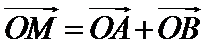
知识点
9.已知点A,B,C在圆


最大值为
正确答案
解析
由题意得,AC为圆的直径,故可设






考查方向
解题思路
先由题意得到AC为圆的直径,后设出所需要点的坐标后把所求的结果表示成函数的形式后求其最值即可。
易错点
1.不会转化题中的条件
知识点
11.如图,在




正确答案
解析






考查方向
解题思路
平面向量的数量积计算问题,往往有两种形式,一种是数量积的定义,而是利用数量积的坐标运算公式,涉及几何图形的问题,可利用几何性质用一组已知基底数量积表示所求数量积。
易错点
1、本题易直接使用数量积的定义,而不知如何计算夹角。
2、不会选择一组基底,从而用向量的加减运算及利用几何性质用一组已知基底数量积表示所求数量积
知识点
14.已知向量a=(x-1,2),b=(4,y),若a⊥b,则点P(x,y)到原点的距离的最小值为___________.
正确答案

解析
由已知得

考查方向
解题思路
本题考查向量数量积的坐标运算,根据已知得到一个二元一次方程,最后转化为原点到这条直线的距离来解答。
易错点
点p到原点的距离不知道怎么来解答。
知识点
7.已知
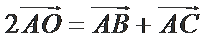
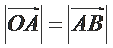
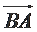
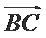
正确答案
解析
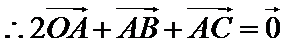
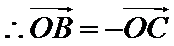
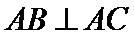
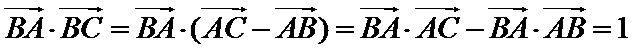
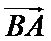
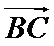
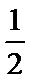
考查方向
解题思路
利用向量的运算法则将已知等式化简,对三角形的形状进行探究,利用运算法则展开求出投影,选出正确的选项
易错点
计算错误
知识点
15.在△ABC中,BC=2,若对任意的实数t, |t





正确答案
8,
解析
考查方向
解题思路
由题意可得在线段BC上存在一点D,使得AD最小,且有AD⊥BC,取得最小值3,设BD=x,CD=2-x,运用勾股定理和向量数量积的定义和余弦定理,结合二次函数的最值的求法,即可得到最值.
易错点
在求最值时候构造函数问题。
知识点
15.在正方形





正确答案
[4,8-2
解析
设CN=x,CM=y,

因为

















考查方向
解题思路
画出正方形,设CN=x,CM=y,将

易错点
处理变量之间的整体关系及转化
知识点
15.





正确答案
解析
3

(3


因为P为内心,所以|PA|=|PB|=|PC|=1
所以

|AB|=
考查方向
平面向量
解题思路
先考虑P是内心,再由题目条件进行分析,找出关系。
易错点
思路不清,直接分解,或者计算错误。
教师点评
本题要求学生能够熟练掌握向量部分的知识与解析几何知识的相互联系,会对题目条件进行分析化简。
知识点
12.已知O,N,P在⊿ABC所在平面内,且

正确答案
解析
考查方向
解题思路
知识点
扫码查看完整答案与解析