- 向量在几何中的应用
- 共120题
如图,焦距为2的椭圆D的两个顶点分别为



(1)求椭圆D的标准方程;
(2)过点

正确答案
(1)
(2)
解析
(1)设椭圆E的标准方程为






∴

(2)设


消去y,得,
∴



∵以PQ为直径的圆经过原点O ∴

又
由


∴
知识点
若直线





正确答案
解析
由



知识点
设F为抛物线E: 

(1)求抛物线方程;
(2)设动直线l与抛物线E相切于点P,与直线
正确答案
见解析
解析
解析:(1)由



(2)设点P(




切线方程:y-

由

设M(0,










故以PQ为直径的圆过y轴上的定点M(0,1)
知识点
已知正方形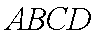
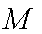
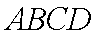
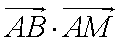
正确答案
4
解析
略
知识点
已知圆锥曲线


(1)求曲线
(2)设曲线






(3)在条件(2)下,如果




正确答案
(1)
(2)
(3)m=4
解析
(1)由



故双曲线

(2)设

从而有:
(3)因为
整理得

注意到



设

又




但当
所以
知识点
如图,非零向量


正确答案
解析
略
知识点
21.已知椭圆





(1)求椭圆
(2)若点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设M是△ABC的重心,若A=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.
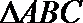
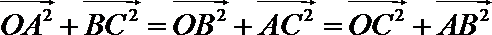
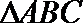
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,在平行四边形




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析






















