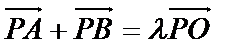- 向量在几何中的应用
- 共120题
1
题型:简答题
|
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
向量在几何中的应用等比数列的判断与证明抛物线的标准方程和几何性质直线与圆锥曲线的综合问题圆锥曲线中的探索性问题
1
题型:简答题
|
20. 已知点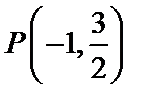

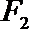
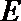
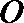
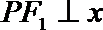
(1)求椭圆
(2)设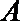
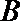


正确答案
解:(1)∵PF1⊥x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|=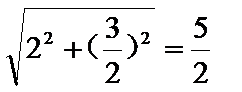
椭圆E的方程为:
(2)设A(x1,y1)、B(x2,y2),由 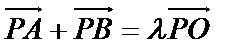
(x1+1,y1-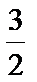
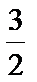
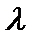
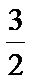
所以x1+x2=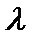
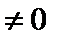
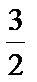
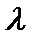
又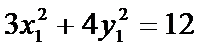
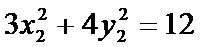
两式相减得3(x1+x2)(x1-x2)+ 4(y1+y2)(y1-y2)=0………..②
以①式代入可得AB的斜率k=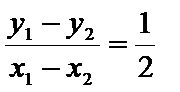
解析
解析已在路上飞奔,马上就到!
知识点
向量在几何中的应用椭圆的定义及标准方程直线与圆锥曲线的综合问题圆锥曲线的定点、定值问题
1
题型:填空题
|
15.在△ABC和△AEF中,B是EF的中点,AB=EF=1,BC=6,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
平面向量数量积的运算数量积表示两个向量的夹角向量在几何中的应用
1
题型:
单选题
|
9.O是


正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
平面向量数量积的运算向量在几何中的应用
1
题型:简答题
|
17.在△ABC中,内角A,B,C的对边分别为a,b,c,已知a,b,c成等比数列,且
(1)若
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理余弦定理平面向量数量积的运算向量在几何中的应用
下一知识点 : 平面向量的综合题
扫码查看完整答案与解析