- 圆锥曲线中的探索性问题
- 共34题
21.已知椭圆





(1)求椭圆
(2)若动直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.在平面直角坐标系



(1)求椭圆C的方程;
(2)设椭圆C的上下顶点分别为



(3)在椭圆C上,是否存在点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
20.设椭圆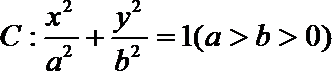
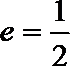
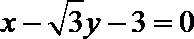
(I)求椭圆C的方程;
(II)在(I)的条件下,过右焦点F2作斜率为k的直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.在平面直角坐标系



(1)求椭圆C的方程;
(2)设椭圆C的上下顶点分别为



(3)在椭圆C上,是否存在点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析











