- 导数的几何意义
- 共154题
21.已知函数
(1)求函数
(2)若


正确答案
(1)
当
递增区间为(-1,1),递减区间为
当

(2)
假设直线

则
而
∴直线

解析
解析已在路上飞奔,马上就到!
知识点
18. 甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女。
(Ⅰ)若从甲校和乙校报名的教师中各任选1名,求选出的2名教师性别相同的概率;
(Ⅱ)若从报名的6名教师中任选2名,并求选出的2名教师来自同一学校的概率。
正确答案
(I)设“从甲校和乙校报名的的教师中任选一名,选出的2名教师性别相同”为事件A,则
(II)设“从报名的6名教师中任选2名,选出的2名教师来自同一学校”为事件B,则
解析
解析已在路上飞奔,马上就到!
知识点
13. 函数

正确答案
y=4x-4
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数


(1)若

(2)若直线




(3)若在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.曲线

正确答案
y=3x+1
解析
解析已在路上飞奔,马上就到!
知识点
20.设

(1)若

(2)若函数



(3)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知


(1)求通项
(2)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设函数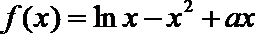
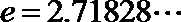
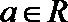
(Ⅰ)当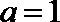
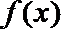
(Ⅱ)若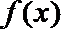
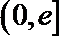
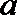
(Ⅲ)设函数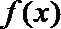
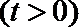
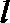
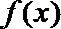
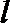
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在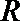
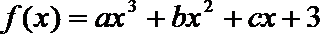
① 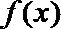
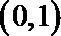
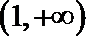
② 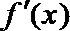
③ 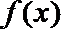
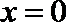
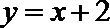
(1)求函数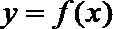
(2)设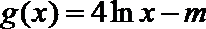
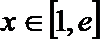
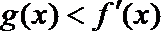
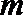
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析