导数的运算
共307题

· 导数的运算

导数的运算
共307题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 4 分

函数的定义域为A，若且时总有，则称为单函数，例如，函数=2x+1()是单函数，下列命题：

①函数（xR）是单函数；

②指数函数（xR）是单函数；

③若为单函数，且，则；

④在定义域上具有单调性的函数一定是单函数。

其中的真命题是_________，（写出所有真命题的编号）

正确答案

②③④

解析

对于①，若，则，不满足；②是单函数；命题③实际上是单函数命题的逆否命题，故为真命题；根据定义，命题④满足条件。

知识点

导数的运算

题型：填空题

填空题 · 4 分

若函数的反函数为，则

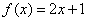
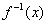
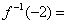
正确答案

解析

略

知识点

导数的运算

题型：单选题

单选题 · 5 分

已知双曲线的一条渐近线平行于直线双曲线的一个焦点在直线上，则双曲线的方程为（）

正确答案

解析

依题意得，所以，

知识点

导数的运算

题型：单选题

单选题 · 5 分

设全集为，集合，则( )

正确答案

解析

，所以

知识点

导数的运算

题型：简答题

简答题 · 12 分

已知函数。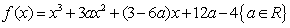

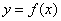
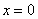
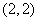
（1）证明：曲线在处的切线过点；

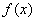
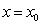
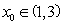
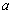
（2）若在处取得极小值，，求的取值范围。

正确答案

见解析。

解析

（1）。

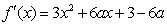
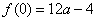
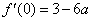
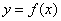
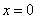
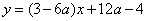
由，得曲线在处的切线方程为

，

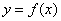
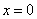
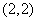
由此知曲线在处的切线过点。

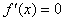
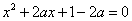
（2）由得.

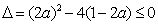
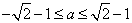
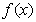
（i）当时，，没有极小值；

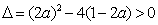
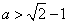
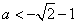
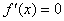
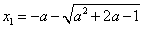
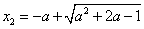
（ii）当时，或，由得

，，

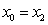
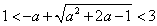
故，由题设知。

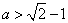
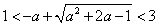
当时，不等式无解；

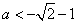
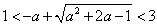
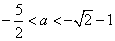
当时，解不等式得。

综合（i）（ii）得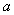的取值范围是。

知识点

导数的运算

题型：简答题

简答题 · 13 分

设椭圆（）的左、右焦点为，右顶点为，上顶点为.已知.

（1）求椭圆的离心率；

（2）设为椭圆上异于其顶点的一点，以线段为直径的圆经过点，经过点的直线与该圆相切于点，，求椭圆的方程。

正确答案

解析

知识点

导数的运算

题型：填空题

填空题 · 5 分

某校早上8：00上课，假设该校学生小张与小王在早上7:30—7:50之间到校，且每人在该时间段的任何时间到校是等可能的，则小张比小王至少早5分钟到校的概率为__ _

（用数字作答）

正确答案

解析

记为时刻，小张，小王到校的时刻分别为，则

这样的二维变量可与点建立对应，满足条件的形成一个边长为的正方形区域。由已知小张比小王至少早5分钟满足关系：，由线性规划知此时形成一个三角形区域，其面积为，故所求概率为：

知识点

导数的运算

题型：简答题

简答题 · 12 分

已知是首相为1，公差为2的等差数列，表示的前项和.

（1）求及；

（2）设是首相为2的等比数列，公比满足，求的通

项公式及其前项和.

正确答案

见解析

解析

（1）由已知

（2）由于，故公比满足

故，

知识点

导数的运算

题型：简答题

简答题 · 13 分

如下图，四棱锥中，底面是以为中心的菱形，底面，，为上一点，且.

（1）证明：平面；

（2）若，求四棱锥的体积.

正确答案

略。

解析

（1）证明：由知为等边三角形，故,

在中，,由余弦定理可求出，

因为,

因为底面

因为,所以平面

（2）设，则，

在中由余弦定理

因为，所以为直角三角形，由勾股定理：

，解出

四棱锥的体积

知识点

导数的运算

继续学习学习下一知识点

下一知识点 : 导数的加法与减法法则

百度题库 > 高考 > 文科数学 > 导数的运算

扫码查看完整答案与解析