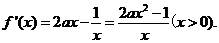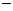导数的几何意义
共154题

· 导数的几何意义

导数的几何意义
共154题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 12 分

已知函数.

（I）当时，求曲线在处的切线方程；

(II)若当时，，求的取值范围.

正确答案

（I）的定义域为.当时，

，曲线在处的切线方程为

（II）当时，等价于

令，则

，

（i）当，时，，故在上单调递增，因此；

（ii）当时，令得

，

由和得，故当时，，在单调递减，因此.

综上，的取值范围是

知识点

导数的几何意义导数的运算利用导数求参数的取值范围

题型：单选题

单选题 · 5 分

已知a函数f(x)=x3-12x的极小值点，则a=（　　　）

A-4

B-2

正确答案

知识点

导数的几何意义利用导数求函数的极值

题型：填空题

填空题 · 14 分

设函数f(x)=ax2－a－lnx，g(x)=－，其中a∈R，e=2.718…为自然对数的底数。

（Ⅰ）讨论f(x)的单调性；

（Ⅱ）证明：当x＞1时，g(x)＞0；

（Ⅲ）确定a的所有可能取值，使得f(x)＞g(x)在区间（1，+∞）内恒成立。

正确答案

（I）

<0，在内单调递减.

由=0，有.

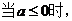
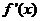
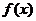
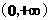
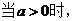
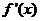
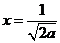
当时，<0，单调递减；

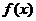
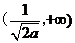
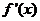
当时，>0，单调递增.

（II）令=，则=.

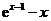
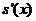
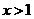
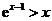
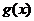
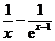
当时，>0，所以，从而=>0.

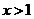
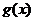
（iii）由（II），当时，>0.

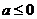
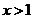
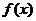
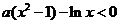
当，时，=.

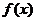
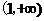
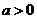
故当>在区间内恒成立时，必有.

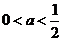
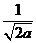
当时，>1.

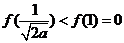
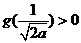
由（I）有,从而，

所以此时>在区间内不恒成立.

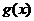
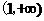
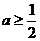
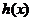
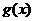
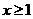
当时，令=().

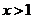
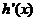
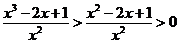
当时，=.

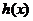
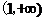
因此在区间单调递增.

又因为=0，所以当时，=>0，即>恒成立.

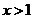
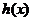
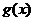
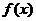
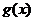
综上，.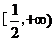

知识点

导数的几何意义利用导数研究函数的单调性利用导数求参数的取值范围

题型：简答题

简答题 · 12 分

20. 已知函数.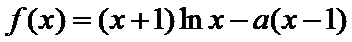

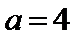
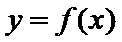
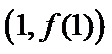
（I）当时，求曲线在处的切线方程；

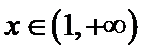
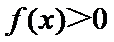
(II)若当时，，求的取值范围.

正确答案

知识点

导数的几何意义利用导数研究函数的单调性利用导数证明不等式

题型：单选题

单选题 · 5 分

设直线l1，l2分别是函数f(x)= 图象上点P1，P2处的切线，l1与l2垂直相交于点P，且l1，l2分别与y轴相交于点A，B则则△PAB的面积的取值范围是

A(0,1)

B(0,2)

C(0,+∞)

D(1,+ ∞)

正确答案

知识点

导数的几何意义

继续学习学习下一知识点

下一知识点 : 导数的运算

百度题库 > 高考 > 文科数学 > 导数的几何意义

扫码查看完整答案与解析