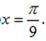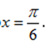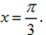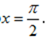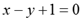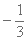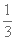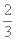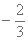- 导数的几何意义
- 共154题
通过随机询

参照右上附表,得到的正确结论
正确答案
解析
略
知识点
已知曲线



正确答案
解析
略
知识点

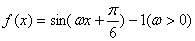
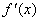
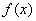
正确答案
解析
略
知识点
已知函数


(1)求证:函数


(2)若函数


正确答案
见解析
解析
(1)由已知可得

又



令






(2)



由二次函数图象性质可得
即


综上,

知识点
已知函数


(1)求实数
(2)设
①若


②是否存在点



正确答案
见解析
解析
(1)








(2)①



在
令

设






②由


表明:若点


而线段



这也表明存在点


则这两个封闭图形面积相等, ————13分
知识点
从某批产品中,有放回地抽取产品2次,每次随机抽取1件,假设事件
(1)求从该批产品中任取1件是二等品的概率P
(2)若该批产品共100件,从中一次性任意抽取2件,用

正确答案
见解析。
解析
(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件是二等品”,则A0、A1互斥,且A=A0+A1。
故P (A)=P (A0+A1)=P (A0) +P (A1)=(1-p)2+C
依题意,知1-p2=0.96,又p>0,得p=0.2。
(2)ξ可能的取值为0,1,2。
若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件,故
P(ξ=0)=

P(ξ=2)=
所以ξ的分布列为

知识点
已知函数





(1)求
(2)若函数

正确答案
见解析。
解析
(1)由





又∵曲线


由<1><2><3>可求得,
(2)若函数




∴方程
解得:

所以当实数


知识点
曲线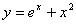
正确答案
解析
略
知识点
已知曲线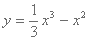
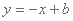
正确答案
解析
略
知识点
已知f (x) = x3 – ax,x∈R,在x = 2处的切线垂直于直线x + 9y – 1 = 0, 则a =( )
正确答案
解析
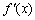
则k=9,∴12-a=9,即a=3。
知识点
扫码查看完整答案与解析