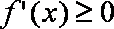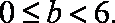- 导数的几何意义
- 共154题
已知曲线

正确答案
解析
设切点的横坐标为(x0,y0)
∵曲线

∴y′=


故选A,
知识点
在一次课内比教学活动中9位评委给某参赛教师的分数如下图所示,记分员在去掉一个最高分和一个最低分后,算出平均分为92分,复核员在复核时发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字
正确答案
5
解析
根据茎叶图运算,直接得出结果。
知识点
已知函数


(1)求

(2)对函数



正确答案
见解析
解析
解析:
(1)由
而点


又直线
故有
(2)由(1)得
由

令
令
故

故当

当
从而当





故
要使



知识点
设曲线






(1)求
(2)求函数
(3)求证:
正确答案
见解析。
解析
(1)



(2)


又

(3)证明:
∴原式





知识点
过点(﹣1,0)与函数f(x)=ex(e是自然对数的底数)图象相切的直线方程是 。
正确答案
y=x+1
解析
设切点为(a,ea)
∵f(x)=ex,∴f′(x)=ex,
∴f′(a)=ea,
所以切线为:y﹣ea=ea(x﹣a),代入点(﹣1,0)得:
﹣ea=ea(﹣1﹣a),
解得a=0
因此切线为:y=x+1。
知识点
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,若数列
正确答案
解析
由f(x)=x2+bx求导得:f′(x)=2x+b,
∵函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,
∴f′(1)=2+b=3,∴b=1,∴f(x)=x2+x
所以f(n)=n(n+1),
∴
∴S2013的值为1﹣





知识点
已知函数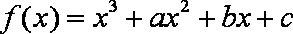
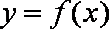
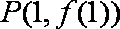
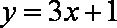
(1)若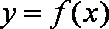
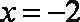
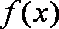
(2)若函数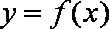
正确答案
见解析。
解析
(1)由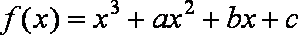
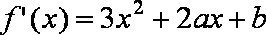
过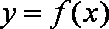
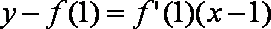
即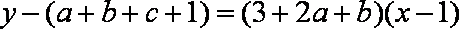
而过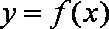
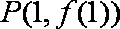
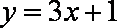
故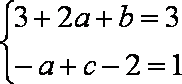
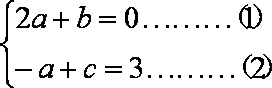
因为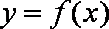
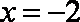
故
由(1)(2)(3)联立解得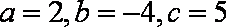
所以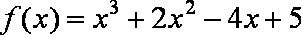
(2)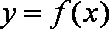
又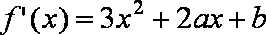
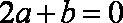
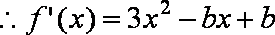
依题意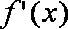
即
①在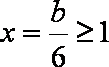
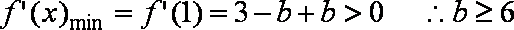
②在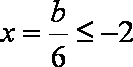
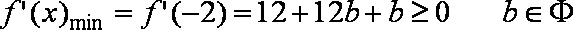
③在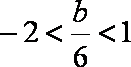
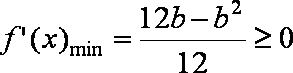
综合上述讨论可知,所求参数b的取值范围是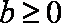
知识点
设函数f(x)=ex﹣ax﹣2
(1)求f(x)的单调区间
(2)若a=1,k为整数,且当x>0时,(x﹣k) f´(x)+x+1>0,求k的最大值。
正确答案
见解析
解析
解:(1)函数f(x)=ex﹣ax﹣2的定义域是R,f′(x)=ex﹣a,
若a≤0,则f′(x)=ex﹣a≥0,所以函数f(x)=ex﹣ax﹣2在(﹣∞,+∞)上单调递增。
若a>0,则当x∈(﹣∞,lna)时,f′(x)=ex﹣a<0;
当x∈(lna,+∞)时,f′(x)=ex﹣a>0;所以,f(x)在(﹣∞,lna)单调递减,在(lna,+∞)上单调递增。
(2)由于a=1,所以,(x﹣k) f´(x)+x+1=(x﹣k) (ex﹣1)+x+1
故当x>0时,(x﹣k) f´(x)+x+1>0等价于k<
令g(x)=
由(1)知,函数h(x)=ex﹣x﹣2在(0,+∞)上单调递增,而h(1)<0,h(2)>0,
所以h(x)=ex﹣x﹣2在(0,+∞)上存在唯一的零点,故g′(x)在(0,+∞)上存在唯一的零点,设此零点为α,则有α∈(1,2)
当x∈(0,α)时,g′(x)<0;当x∈(α,+∞)时,g′(x)>0;所以g(x)在(0,+∞)上的最小值为g(α),又由g′(α)=0,可得eα=α+2所以g(α)=α+1∈(2,3)
由于①式等价于k<g(α),故整数k的最大值为2
知识点
已知函数
(1)若


(2)若

正确答案
(1)
(2)
解析
(1)由


所以

所以所求切线方程为
即
(2)由已知

因为函数

即不等式

令

当


当


由此得


知识点
已知函数


(1)若曲线



(2)当

正确答案
见解析。
解析
由题意得:

(1)由曲线





(2)设


令




从而函数



当




当




综上可知,当





知识点
扫码查看完整答案与解析