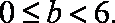- 导数的几何意义
- 共154题
已知曲线

正确答案
解析
设切点的横坐标为(x0,y0)
∵曲线

∴y′=


故选A,
知识点
设曲线






(1)求
(2)求函数
(3)求证:
正确答案
见解析。
解析
(1)



(2)


又

(3)证明:
∴原式





知识点
过点(﹣1,0)与函数f(x)=ex(e是自然对数的底数)图象相切的直线方程是 。
正确答案
y=x+1
解析
设切点为(a,ea)
∵f(x)=ex,∴f′(x)=ex,
∴f′(a)=ea,
所以切线为:y﹣ea=ea(x﹣a),代入点(﹣1,0)得:
﹣ea=ea(﹣1﹣a),
解得a=0
因此切线为:y=x+1。
知识点
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,若数列
正确答案
解析
由f(x)=x2+bx求导得:f′(x)=2x+b,
∵函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x﹣y+2=0平行,
∴f′(1)=2+b=3,∴b=1,∴f(x)=x2+x
所以f(n)=n(n+1),
∴
∴S2013的值为1﹣





知识点
已知函数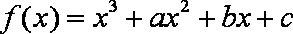
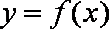
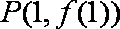
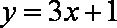
(1)若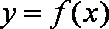
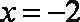
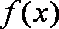
(2)若函数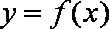
正确答案
见解析。
解析
(1)由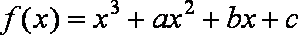
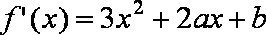
过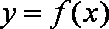
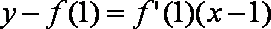
即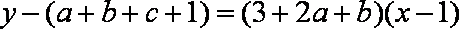
而过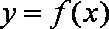
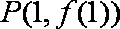
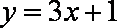
故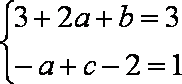
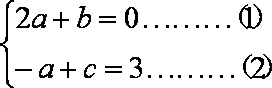
因为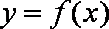
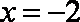
故
由(1)(2)(3)联立解得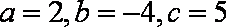
所以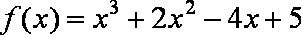
(2)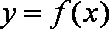
又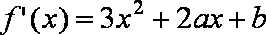
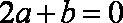
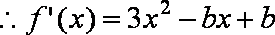
依题意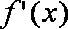
即
①在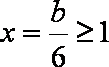
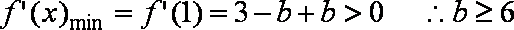
②在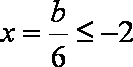
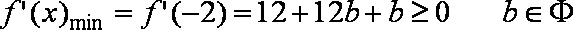
③在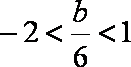
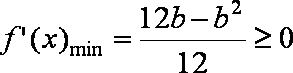
综合上述讨论可知,所求参数b的取值范围是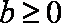
知识点
扫码查看完整答案与解析