- 导数的几何意义
- 共154题
21.已知函数

(Ⅰ)设曲线


(Ⅱ)当


(Ⅲ)令




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
14.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(I)求实数
(II)求

(III)对任意给定的正实数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1) 求函数
(2) 若函数






(3) 求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)求
(Ⅱ)当





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:定义在R上的函数
(1)若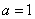
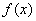
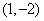
(2)若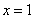
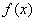
(3)若函数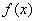

正确答案
解:(1)当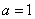
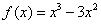
则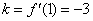
∴切线方程: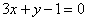
(2)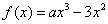
∵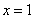
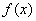
∴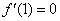
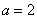
(3)①当a=0时,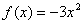
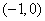
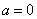
②当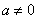
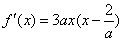
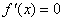
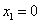
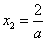
当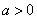
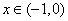
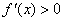
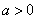
当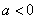
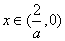

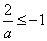

综上所述,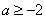
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析