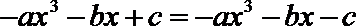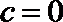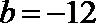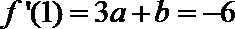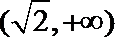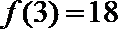- 导数的几何意义
- 共154题
1
题型:填空题
|
13.若曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义两条直线垂直与倾斜角、斜率的关系直线的一般式方程
1
题型:简答题
|
17.设函数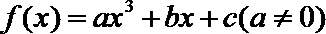
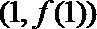
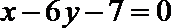
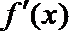
(1)求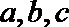
(2)求函数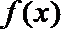
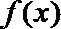
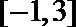
正确答案
(1)∵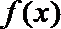
∴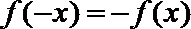
∴
∵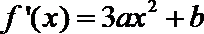
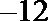
又直线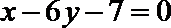

∴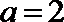
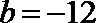
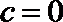
(2)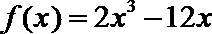
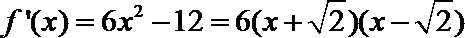
所以函数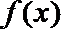
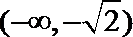
∵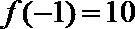
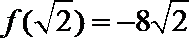
∴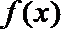
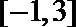
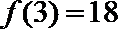
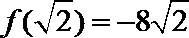
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义利用导数研究函数的单调性利用导数求函数的最值两条直线垂直与倾斜角、斜率的关系
1
题型:简答题
|
22.已知函数

(1)求函数
(2)若直线


(3)设



正确答案
解:(1)

在区间




所以,



(2)设切点坐标为
则
解得

(3)
则
解

所以,在区间

在区间

当



所以

当



所以

当



综上所述,当


当



当


解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义利用导数研究函数的单调性利用导数求函数的最值
1
题型:简答题
|
18.


(1)求

(2)求切点坐标,求直线
正确答案
(1)k=-3
(2)设切点为
切线的斜率
代入到

解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义导数的运算两条直线垂直与倾斜角、斜率的关系
1
题型:
单选题
|
5.曲线


正确答案
A
解析
解析已在路上飞奔,马上就到!
知识点
导数的几何意义
下一知识点 : 导数的运算
扫码查看完整答案与解析