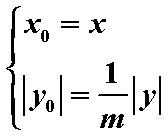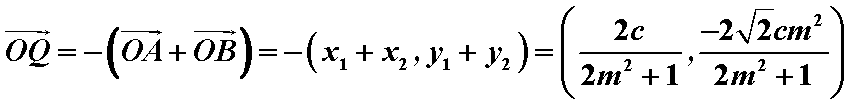- 直线与椭圆的位置关系
- 共59题
已知椭圆





(1)求椭圆
(2)若




正确答案
见解析
解析
(1)设点

则
故

所以
故
所以椭圆

(2)设


又


又圆


故圆

即
也就是
令

故圆


(另法:(1)中也可以直接将点

知识点
设P是圆x2+y2=4上的任意一点,过P作x轴的垂线段PD,D为垂足, M是线段PD上的点,且满足|DM|=m|PD|(0<m<1),当点P在圆上运动时,记M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过曲线C的左焦点F作斜率为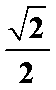
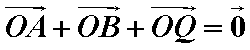
正确答案
见解析
解析
(1)如图设M(x,y)、P(x0,y0),则由|DM|=m|PD|(0<m<1)得
x= x0,|y|=m| y0|,即
∵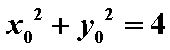
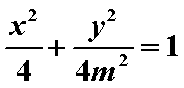
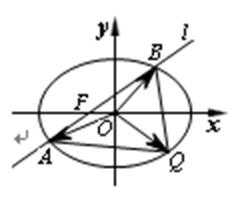
(2)设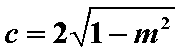
由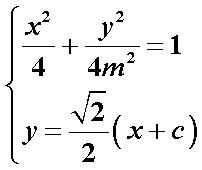
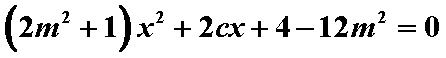
设A(x1,y1)、B(x2,y2).
则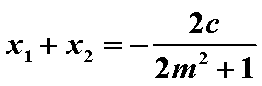
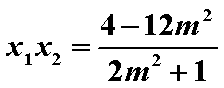
∴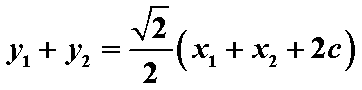
∵
即Q点坐标为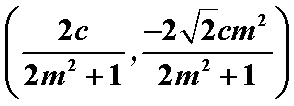
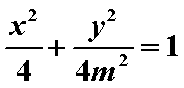
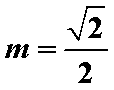
∴存在当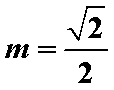
知识点
已知椭圆







(1)求椭圆
(2)设椭圆






正确答案
见解析
解析
(1)当


解得:

(2)当








证明如下:设点M,N点的坐标分别是


所以点



由方程组

所以:
从而:
所以:以


知识点
椭圆





(1)求椭圆
(2)若椭圆上两点


正确答案
见解析
解析
(1)因为椭圆



又以

又
得

而


故椭圆

(2)法一:设点

则

由
所以

将


法二:设点
则
两等式相减得
将

知识点
若圆


(1)求a,b的值;
(2)判断矩阵A是否可逆,如果可逆,求矩阵A的逆矩阵A-1,如不可逆,说明理由.
正确答案
见解析
解析
(1)设点


则
因为点



又圆方程为






(2)

所以
知识点
扫码查看完整答案与解析