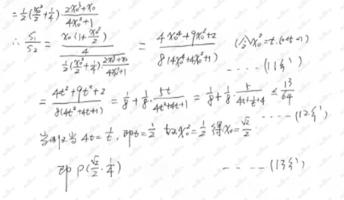- 直线与椭圆的位置关系
- 共59题
21.(本小题满分14分)
平面直角坐标系
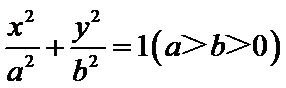
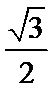
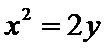
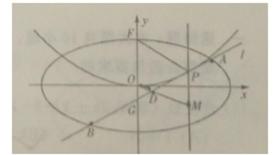
(I)求椭圆C的方程;
(II)设P是E上的动点,且位于第一象限,E在点P处的切线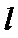
(i)求证:点M在定直线上;
(ii)直线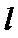
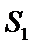
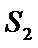
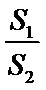
正确答案
知识点
20.阅读下面的材料,根据要求写一篇不少于800字的文章。
近年来,以奇山异水和悠久历史文化而闻名的某旅游城市,虽然其市区公共交通在不断完善,可自从限摩以后,在私家车迅猛增多的同时,还有不少市民选择骑电动车出行。为初步有效管理这种“新型”交通工具,市某综合管理部门曾于前两年给这些超标电动车(行驶速度大于每小时20公里、车身总重量大于40公斤等指标)上了牌照,算是给予它们临时合法的出行身份,但是牌照有效期到今年2月底止,这也就是说,从今年3月1日起,该市城区4万多辆超标电动车已被禁行,违者将受到严厉的处罚。
一方面是诸多管理的必要,一方面是便捷出行的需求;事实上要彻底禁行这几万辆超标电动车,管理者和骑行者都会感到很不容易。
假定你也是在该市市区生活的市民,请以管理部门代言人或超标电动车骑行者身份就禁行超标电动车这事表达你的看法。
要求选定你的写作身份,选好角度,确定立意,明确文体,自拟标题;不要脱离材料内容及含意的范围作文,不要套作,不得抄袭。
正确答案
略
解析
这则材料需要考生首先明确写作身份,是要以骑行者的身份来谈对禁行超标电动车这件事的看法,还是要以管理部门代言人的身份来谈对这件事的看法,不能两种角度都谈。但无论你选择哪一方,都因首先说明你支持或不支持的原因,然后分析其利弊,需要注意的是在分析利弊的时候不能只站在个人的角度,而应从整体出发,从对整个市区影响的角度去看待问题。论证时要有理有据,论据要真实,不能只是空发牢骚。
所以可以这样构思:确定身份,明确看法,说出原因,分析利弊,提出解决问题的办法。只要能自圆其说即可。
考查方向
解题思路
审清题意,确定立意,查找论据,完成作文。
易错点
此题审题不难,但考生容易陷入空谈,不能有充分的论据证明其观点。
知识点
9.已知直线:


正确答案
解析
直线:y=kx-k+1恒过定点(1,1),利用直线:y=kx-k+1与曲线C:
考查方向
曲线与方程
解题思路
根据等量关系,建立方程,然后求出参数的取值范围
易错点
计算化简错误
知识点
(本小题满分14分)
已知点

(Ⅰ)设椭圆的两个焦点分别为



(Ⅱ)若直线









正确答案
考查方向
易错点
1、未注意到点
知识点
18.如图,在平面直角坐标系xOy中,已知椭圆

(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
正确答案
(1)由题意,得

解得


所以椭圆的标准方程为
(2)当


当





将

则



若


从而


则


因为


此时直线


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析