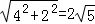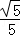- 导数的乘法与除法法则
- 共1249题
已知抛物线
A
B1
C2
D4
正确答案
解析
本题考查抛物线的相关几何性质及直线与圆的位置关系
法一：抛物线y2＝2px（p>0）的准线方程为
法二：作图可知，抛物线y2＝2px（p>0）的准线与圆（x－3）2＋y2＝16相切与点（-1,0）
所以
知识点
在平面直角坐标系中，点0（0，0），P（6，8），将向量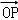
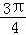
A（﹣7
B（﹣7
C（﹣4 ，﹣2）
D（﹣4 ，2）
正确答案
解析
∵点0（0，0），P（6，8），
∴
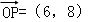
设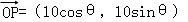
则cosθ=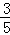
∵向量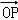
∴
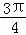
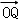
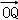
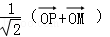
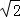
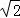
知识点
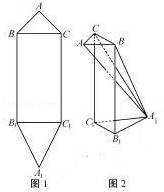
平面图形ABB1A1C1C如图1所示，其中BB1C1C是矩形，BC=2，BB1=4，AB=AC=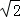
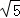
（1）证明：AA1⊥BC；
（2）求AA1的长；
（3）求二面角A﹣BC﹣A1的余弦值。
正确答案
见解析
解析
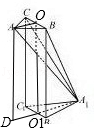
（1）证明：取BC，B1C1的中点为点O，O1，连接AO，OO1，A1O，A1O1，
∵AB=AC，∴AO⊥BC
∵平面ABC⊥平面BB1C1C，平面ABC∩平面BB1C1C=BC
∴AO⊥平面BB1C1C
同理A1O1⊥平面BB1C1C，∴AO∥A1O1，∴A、O、A1、O1共面
∵OO1⊥BC，AO⊥BC，OO1∩AO=O，∴BC⊥平面OO1A1A
∵AA1⊂平面OO1A1A，∴AA1⊥BC；
（2）解：延长A1O1到D，使O1D=OA，则∵O1D∥OA，∴AD∥OO1，AD=OO1，
∵OO1⊥BC，平面A1B1C1⊥平面BB1C1C，平面A1B1C1∩平面BB1C1C=B1C1，
∴OO1⊥面A1B1C1，
∵AD∥OO1，
∴AD⊥面A1B1C1，
∵AD=BB1=4，A1D=A1O1+O1D=2+1=3
∴AA1=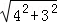
（3）解：∵AO⊥BC，A1O⊥BC，∴∠AOA1是二面角A﹣BC﹣A1的平面角
在直角△OO1A1中，A1O=
在直角△OAA1中，cos∠AOA1=﹣
∴二面角A﹣BC﹣A1的余弦值为﹣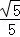
知识点
右图是求样本
AS=S+
BS=S+
CS=S+n
DS=S+
正确答案
解析
略
知识点
已知函数
A
B
C
D
正确答案
解析
画出
知识点
扫码查看完整答案与解析