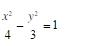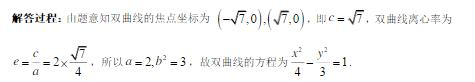椭圆的几何性质
共137题

· 椭圆的几何性质

椭圆的几何性质
共137题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

如图，已知椭圆过点. ，离心率为，左、右焦点分别为、 .点为直线上且不在轴上的任意一点，直线和与椭圆的交点分别为、和、，为坐标原点。

（1）求椭圆的标准方程；

（2）设直线、的斜线分别为、.

（i）证明：；

（ii）问直线上是否存在点，使得直线、、、的斜率、、、满足？若存在，求出所有满足条件的点的坐标；若不存在，说明理由。

正确答案

见解析。

解析

（1）解：因为椭圆过点（1，），e=，

所以，.

又a2=b2+c2，

所以，故所求椭圆方程为 .

（2）（i）设点P（，），则=，=，因为点不在轴上，所以

，又=2，所以=，

因此结论成立。

知识点

椭圆的几何性质

题型：简答题

简答题 · 13 分

已知椭圆的离心率为，右焦点为，斜率为1的直线与椭圆交于两点，以为底边作等腰三角形，顶点为。

(1) 求椭圆的方程；

(2) 求的面积。

正确答案

(1)1

(2)

解析

（1）由已知得，解得，又。

所以椭圆的方程为。

（2）设直线l的方程为由得。

设、的坐标分别为中点为，则

。

因为是等腰的底边，所以⊥，所以的斜率，解得，此时方程①为，解得。

所以，所以||=，此时，点到直线：的距离，所以的面积。

知识点

椭圆的几何性质

题型：填空题

填空题 · 5 分

设数列是首项为，公比为的等比数列，则

正确答案

解析

由题意知，，，，所以；；

知识点

椭圆的几何性质

题型：填空题

填空题 · 4 分

已知双曲线和椭圆有相同的焦点，且双曲线的离心率是椭圆离心率的两倍，则双曲线的方程为 .

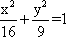
正确答案

解析

知识点

椭圆的几何性质双曲线的定义及标准方程双曲线的几何性质

题型：单选题

单选题 · 5 分

已知a＝log23＋log2，b＝log29－log2，c＝log32，则a，b，c的大小关系是(　　)

Aa＝b＜c

Ba＝b＞c

Ca＜b＜c

Da＞b＞c

正确答案

解析

a＝log23＋＝，b＝log29－＝，因此a＝b，而＞log22＝1，log32＜log33＝1，所以a＝b＞c，故选B项

知识点

椭圆的几何性质

继续学习学习下一知识点

下一知识点 : 椭圆的相关应用

百度题库 > 高考 > 文科数学 > 椭圆的几何性质

扫码查看完整答案与解析