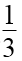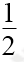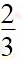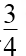- 椭圆的几何性质
- 共137题
21.已知A是椭圆E：
（I）当
(II) 当2
正确答案
知识点
20．
已知椭圆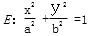
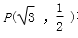
(Ⅰ)求椭圆E的方程；
(Ⅱ)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D，证明：︳MA︳·︳MB︳=︳MC︳·︳MD︳
正确答案
知识点
11．已知椭圆
A
B2－
C
D
正确答案
解析
设F1A=x, F2A=y,由题可知，x+y=2a,x2+y2=4c2,2x+√2x=4a，联立方程组，代换得a2(9-6√2)=c2,即e=
考查方向
本题主要考查直线与椭圆的位置关系
解题思路
1、用a,c表示出F1A,F2A；
2、将所求式子联立，即可得到结果。A选项不正确，B选项不正确，C选项不正确，所以选D选项。
易错点
本题易在表示a, c关系时发生错误。
知识点
9. 如图，在圆
A
B
C
D
正确答案
解析
如图，设M点坐标（x,y），则P点坐标为(x,2y),因为P点在圆上，所以将P点坐标代入圆的方程得到
椭圆的标准方程得到
考查方向
解题思路
如图，
设M点坐标（x,y），则P点坐标为(x,2y),然后将P点坐标代入圆的方程即得M点的轨迹方程，然后再求离心率
易错点
不会用相关点法求椭圆方程，或求出椭圆方程后
知识点
20．如图，F是椭圆
（1）求该椭圆的标准方程；
（2）若直线l与上下半椭圆分别交于点P、Q，与x轴交于点M，且|PM|=2|MQ|，求△OPQ的面积取得最大值时直线l的方程．
正确答案
（1）
解析
试题分析：本题属于圆锥曲线的综合应用问题，属于拔高题，不容易得分，解析如下：
（1）由题意可得c=
将x=c代入椭圆方程可得y=±b
即有△OP0Q0的面积为
即
（2）设M（t，0），且
直线PQ：x=my+t，代入椭圆方程，
可得（4m2+9）y2+8mty+4t2﹣36=0，
设P（x1，y1），Q（x2，y2），y1+y2=﹣
由|PM|=2|MQ|，可得
t2=
则△OPQ的面积为S=
=6|t|•
当t2=5＜9，此时m2=
故所求直线方程为x=±
考查方向
解题思路
（1）利用相关知识求椭圆方程；
（2）联立方程组，由|PM|=2|MQ|找关系，整理即可求解．
易错点
对题中条件的处理容易出错。
知识点
10. 设椭圆
A
B
C
D
正确答案
解析
在直角三角形
考查方向
解题思路
根据焦距为2c，在直角三角形中将其他两边用c表示出来，再利用椭圆的定义得到一个等式，解出比值就可以得到所求的离心率。
易错点
1、根据已知条件不能转化为a,b,c有关的一个等式。
知识点
7． 若椭圆
A3
B
C21
D84
正确答案
解析
由椭圆和双曲线的定义，得
考查方向
本题主要考查了椭圆和双曲线的定义。
易错点
本题易在利用双曲线定义得到
知识点
3．若实数数列：
A
B
C
D
正确答案
解析
由
考查方向
本题主要考查等比数列的概念和椭圆的离心率的概念。
解题思路
由等比数列求出a,代入圆锥曲线方程求出离心率。
易错点
1、等比数列概念不清导致a 漏负解
2、误认为圆锥曲线只是椭圆导致漏解。
知识点
正确答案
知识点
5.直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l的距离为其短轴长的，则该椭圆的离心率为（）
A
B
C
D
正确答案
知识点
扫码查看完整答案与解析