- 椭圆的几何性质
- 共137题
某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横直线的交叉点以及三角形的顶点）处都种了一株相同品种的作物。根据历年的种植经验，一株该种作物的年收货量
这里，两株作物“相近”是指它们之间的直线距离不超过1米。
（1）完成下表,并求所种作物的平均年收获量;
（2）在所种作物中随机选取一株,求它的年收获量至少为48kg的概率.
正确答案
（1） 46
（2）0.4
解析
（1）由图知，三角形中共有15个格点,
与周围格点的距离不超过1米的格点数都是1个的格点有2个，坐标分别为(4,0),(0,4)。
与周围格点的距离不超过1米的格点数都是2个的格点有4个，坐标分别为(0,0), (1,3), (2,2),(3,1)。
与周围格点的距离不超过1米的格点数都是3个的格点有6个，坐标分别为(1,0), (2,0), (3,0),(0，1,) ,(0，2),(0，3,)。
与周围格点的距离不超过1米的格点数都是4个的格点有3个，坐标分别为(1，1), (1,2), (2,1)。如下表所示：
平均年收获量
（2）在15株中，年收获量至少为48kg的作物共有2+4=6个.
所以，15株中任选一个，它的年收获量至少为48k的概率P=
知识点
设
A
B
C
D
正确答案
解析
∵△
∴
知识点
设抛物线C：y2＝4x的焦点为F，直线l过F且与C交于A，B两点，若|AF|＝3|BF|，则l的方程为( )。
Ay＝x－1或y＝－x＋1
By＝
Cy＝
Dy＝
正确答案
解析
由题意可得抛物线焦点F(1,0)，准线方程为x＝－1.
当直线l的斜率大于0时，如图所示，过A，B两点分别向准线x＝－1作垂线，垂足分别为M，N，则由抛物线定义可得，|AM|＝|AF|，|BN|＝|BF|。
设|AM|＝|AF|＝3t(t＞0)，|BN|＝|BF|＝t，|BK|＝x，而|GF|＝2，
在△AMK中，由
解得x＝2t，则cos∠NBK＝
∴∠NBK＝60°，则∠GFK＝60°，即直线AB的倾斜角为60°。
∴斜率k＝tan 60°＝
当直线l的斜率小于0时，如图所示，同理可得直线方程为y＝
知识点
已知点A（2，0），抛物线C：x2=4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，则|FM|：|MN|=
A2:
B1:2
C1:
D1:3
正确答案
解析
依题意可得AF所在直线方程为
知识点
若a∈R，则“a=1”是“|a|=1”的
正确答案
解析
当a=1时，|a|=1成立，反过来，若|a|=1时，
知识点
设圆锥曲线I的两个焦点分别为F1，F2，若曲线I上存在点P满足
A
B
C
D
正确答案
解析
当曲线为椭圆时
当曲线为双曲线时
知识点
如图，在平面直角坐标系
（1）求椭圆的方程；
（2）设
（i）若
（ii）求证：
正确答案
见解析
解析
（1）由题设知，
∴
由点
∴椭圆的方程为
（2）由（1）得
∴设
∴
∴
同理，
（i）由①②得，
∵注意到
∴直线
（ii）证明：∵
∴
由点
同理。
∴
由①②得，
∴
∴
知识点
已知函数
(1)求
(2)求使 
正确答案
（1） 
（2）
解析
（1）
（2）由（1）知，
知识点
若曲线
正确答案
解析
因为
知识点
设a，b，c均为正数，且a＋b＋c＝1.证明：
(1)ab＋bc＋ca≤
(2)
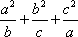
正确答案
见解析
解析
(1)由a2＋b2≥2ab，b2＋c2≥2bc，c2＋a2≥2ca，
得a2＋b2＋c2≥ab＋bc＋ca.
由题设得(a＋b＋c)2＝1，即a2＋b2＋c2＋2ab＋2bc＋2ca＝1.
所以3(ab＋bc＋ca)≤1，即ab＋bc＋ca≤
(2)因为
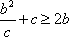
故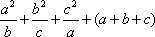
即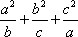
所以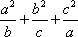
知识点
扫码查看完整答案与解析