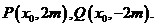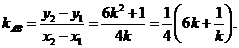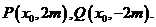- 椭圆的几何性质
- 共137题
19.已知椭圆C:
(I)求椭圆C的方程及离心率;
(II)设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
正确答案
知识点
21.已知椭圆C: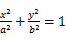

(I)求椭圆C的方程;
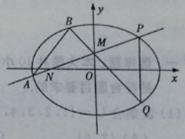
(Ⅱ)过动点M(0,m)(m>0)的直线交x轴与点N,交C于点A,P(P在第一象限),且M是线段PN的中点.过点P作x轴的垂线交C于另一点Q,延长线QM交C于点B.
(i)设直线PM、QM的斜率分别为k、k',证明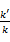
(ii)求直线AB的斜率的最小值.
正确答案
(Ⅰ) 
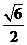
解析
试题分析:(Ⅰ)分别计算a,b即得.
(Ⅱ)(i)设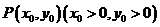
由M(0,m),可得
得到直线PM的斜率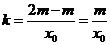
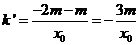
(ii)设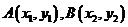
直线PA的方程为y=kx+m,
直线QB的方程为y=-3kx+m.
联立 
整理得
应用一元二次方程根与系数的关系得到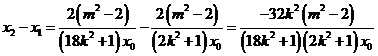
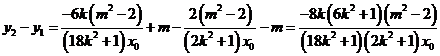
得到
应用基本不等式即得.
试题解析:(Ⅰ)设椭圆的半焦距为c,
由题意知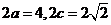
所以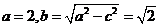
所以椭圆C的方程为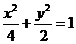
(Ⅱ)(i)设
由M(0,m),可得
所以 直线PM的斜率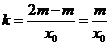
直线QM的斜率
此时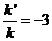
所以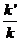
(ii)设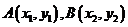
直线PA的方程为y=kx+m,
直线QB的方程为y=-3kx+m.
联立 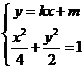
整理得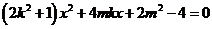
由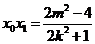
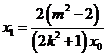
所以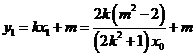
同理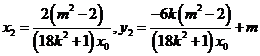
所以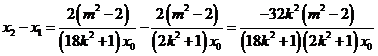
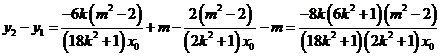
所以
由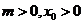
所以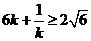
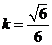
此时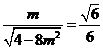

所以直线AB 的斜率的最小值为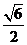
考查方向
知识点
已知A是椭圆E:


(I)当

(II) 当2

正确答案
(Ⅰ)设

由已知及椭圆的对称性知,直线

又


将


解得


因此

(2)将直线



由


由题设,直线


由


设



所以


因此




知识点
已知椭圆E:+=1(a﹥b﹥0)的一个焦点与短轴的两个端点是正三角形的三个顶点,点P(,)在椭圆E上。
(Ⅰ)求椭圆E的方程;
(Ⅱ)设不过原点O且斜率为的直线l与椭圆E交于不同的两点A,B,线段AB的中点为M,直线OM与椭圆E交于C,D,证明:︳MA︳·︳MB︳=︳MC︳·︳MD︳
正确答案
(I)由已知,a=2b.
又椭圆



所以椭圆E的方程是
(II)设直线l的方程为

由方程组

方程①的判别式为



由①得
所以M点坐标为

由方程组

所以
又

所以
知识点
5.直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率()
正确答案
知识点
扫码查看完整答案与解析