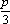- 椭圆的几何性质
- 共137题
若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被录用的概率为 ( )
正确答案
解析
略。
知识点
已知



(1)当


(2)当直线


正确答案
见解析
解析
(1)证明:
因为
所以
因为

所以
将

由①和③消

所以 
(2)当直线

可得

当直线
设直线



联立


由

又
所以
所以 
假设

又因为
所以

化简 


这与①式矛盾,所以假设不成立。
因此对于任意


知识点
“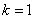
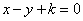
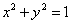
正确答案
解析
略。
知识点
设



的中点在


正确答案
解析
略
知识点
10.如图,设点








正确答案
解析
点P是单位圆上的动点,点






知识点
已知直线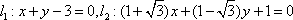
正确答案
解析
略
知识点
已知双曲线C的焦点、实轴端点恰好是椭圆
正确答案
解析
略
知识点
已知点















(1)求椭圆
(2)当


(3)对于动直线


正确答案
见解析
解析
(1)设





(2)

代入





(3)解法一:由于

设
设直线



直线


解法二:由于



设
设直线








知识点
在Rt△ABC中,∠C=90°,∠A=30°,则A、B为焦点,过点C的椭圆的离心率
正确答案
解析
略
知识点
以抛物y2=4x的焦点为圆心且与双曲线
是____
正确答案
解析
略
知识点
扫码查看完整答案与解析