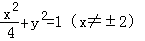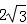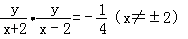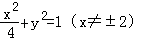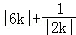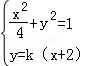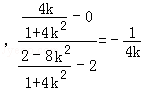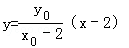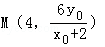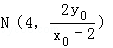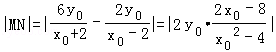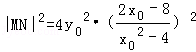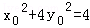- 椭圆的几何性质
- 共137题
已知椭圆C的中心在原点,一个焦点与抛物线x2=4y的焦点相同,点P(1,)是椭圆C是一点,斜率为的直线l交椭圆C于M,N两点,且P,M,N三点不重合。
(1)求椭圆C的方程;
(2)设直线PM、PN的斜率分别为kPM、kPN,求证:kPM + kPN=0;
(3)△PMN的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由。
正确答案
见解析。
解析
知识点
已知椭圆的中心在原点




(1)求这个椭圆的标准方程;
(2)若椭圆上有一点

正确答案
(1)
(2)
解析
(1)由已知,可设椭圆方程为
则 

所以 
所以 椭圆方程为
(2)若直线





于是,设直线



则


所以 
因为 四边形
所以 
所以 点

所以 
解得
所以
知识点
已知动点P到点A(﹣2,0)与点B(2,0)的斜率之积为﹣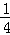
(1)求曲线C的方程;
(2)若点Q为曲线C上的一点,直线AQ,BQ与直线x=4分别交于M、N两点,直线BM与椭圆的交点为D,求线段MN长度的最小值。
正确答案
(1)
(2)
解析
(1)设P(x,y),由题意知 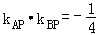
化简得曲线C方程为:
(2)思路一
满足题意的直线AQ的斜率显然存在且不为零,设其方程为y=k(x+2),
由(Ⅰ)知
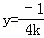
当x=4时得N点坐标为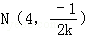
所以
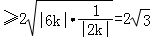
当且仅当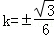
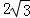
思路二:满足题意的直线AQ的斜率显然存在且不为零,设其方程为y=k(x+2),
联立方程:
消元得(4k2+1)x2+16k2x+16k2﹣4=0,
设Q(x0,y0),M(x1,y1),N(x2,y2),
由韦达定理得: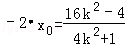
所以
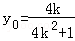
所以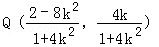
所以直线BQ的斜率为
以下同思路一
思路三:设Q(x0,y0),则直线AQ的方程为
直线BQ的方程为
当x=4,得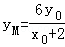
当x=4,得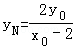
则
又
所以
利用导数,或变形为二次函数求其最小值。
知识点
给定椭圆








(1)求椭圆
(2)点




(ⅰ)当点



(ⅱ)求证:线段
正确答案
见解析
解析
(1)


准圆方程为
(2)(ⅰ)因为准圆


设过点

所以由

因为直线
所以

所以



(ⅱ)①当直线

则

当



此时



同理可证当


②当


设经过点

所以由
得 
由

因为

设


所以

所以

综合①②知:因为



所以线段


所以线段
知识点











正确答案
解析
略
知识点
已知椭圆

(1)求椭圆的方程;
(2)过点A作直线交椭圆于另一点M,求|AM|长度的最大值;
(3)已知定点E(﹣1,0),直线y=kx+t与椭圆交于C、D相异两点,证明:对任意的t>0,都存在实数k,使得以线段CD为直径的圆过E点。
正确答案
见解析。
解析
(1)解:在椭圆中,由已知得
过点A(0,﹣b)和B(a,0)的直线方程为
该直线与原点的距离为

解得:a2=3,b2=1,所以椭圆方程为
(2)解:设M(x,y),则x2=3(1﹣y2),|AM|2=x2+(y+1)2=﹣2y2+2y+4,其中﹣1≤y≤1(6分)
当


(3)证明:将y=kx+t代入椭圆方程,得(1+3k2)x2+6ktx+3t2﹣3=0,
由直线与椭圆有两个交点,所以△=(6kt)2﹣12(1+3k2)(t2﹣1)>0,解得
设C(x1,y1)、D(x2,y2),则

因为以CD为直径的圆过E点,所以
而y1y2=(kx1+t)(kx2+t)=
所以

如果


所以,对任意的t>0,都存在k,使得以线段CD为直径的圆过E点,(14分)
知识点
已知P是以F1、F2为焦点的椭圆


正确答案
解析
由
∴
又知tan∠PF1F2 =
∴
而PF1 + PF2 = 2a,F1F2 = 2c
e =
知识点
在平面直角坐标系





(1)求椭圆
(2)设直线与椭圆





正确答案
见解析
解析
(1)由已知得,由题意得

消去




所以椭圆

(2)结论:直线与圆
证明:由题意可知,直线不过坐标原点,设
(ⅰ)当直线

则

解得

因此,点



半径

(ⅱ)当直线不垂直于
设直线的方程为

得



即
又圆


圆心


将①式带入②式得: 


知识点
设A1、A2为椭圆
点


正确答案
解析
略
知识点
已知焦点在



正确答案
解析
略
知识点
扫码查看完整答案与解析