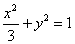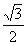- 椭圆的几何性质
- 共137题
已知椭圆



(1)求椭圆C的方程;
(2)对于椭圆C上任一点,若
正确答案
见解析。
解析
知识点
已知椭圆


(1)求椭圆
(2)











正确答案
见解析
解析
(1)由题意可知,


所以椭圆的方程为
(2)由(1)可知,



于是直线



即
又直线



即
所以
又



得


知识点
已知椭圆C:



(1)求椭圆C的离心率e;
(2)用m表示点E,F的坐标;
(3)证明直线EF与y轴交点的位置与m无关。
正确答案
见解析
解析
(1)依题意知


(2)








由


由


(3)据已知,




令x=0,得
知识点
已知椭圆







(1)求椭圆
(2)证明直线

正确答案
见解析
解析
(1)由题意知:
所以,焦点坐标为

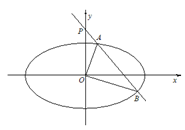
(2)由题意知:直线PB的斜率存在,设直线PB的方程为



由
则
直线AE的方程为


又


把(1)代入(3)式,整理得


知识点
过椭圆







正确答案
解析
略
知识点
若m是2和8的等比中项,则圆锥曲线x2+
正确答案
解析
依题意可知m=
当m=4时,曲线为椭圆,a=2,b=1,则c=

当m=-4时,曲线为双曲线,a=1,b=2,c=
故选D
知识点
已知椭圆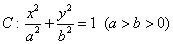
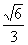
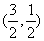
(1)求椭圆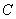
(2)过点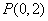
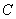
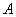
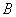
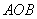
大值。
正确答案
(1)
(2)△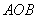
解析
(1)解: 由 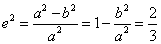
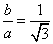
由椭圆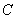
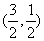
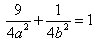
联立① ②,解得 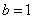
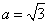
所以椭圆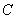
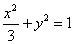
(2)解:易知直线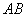
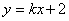
将直线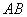
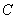
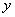
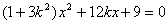
令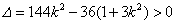
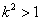
设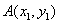
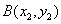
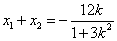
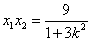
所以 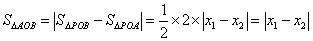
因为 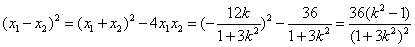
设 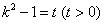
则 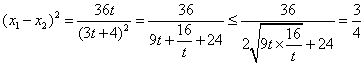
当且仅当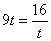
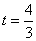
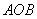
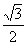
知识点
椭圆



正确答案
解析
略
知识点
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N
在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,
直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵
坐标从大到小依次为A,B,C,D.
(1)设


(2)当e变化时,是否存在直线l,使得BO∥AN,并说明理由.
正确答案
见解析。
解析
(1)因为C1,C2的离心率相同,故依题意可设
设直线

当

(2)t=0时的l不符合题意.

因为
所以当
当
知识点
在平面直角坐标系















(1) 求椭圆
(2)设直线






正确答案
(1)
(2)存在,
解析
(1)设椭圆的方程为



解得

所以椭圆的方程为
(2)直线

由




设椭圆的弦








设


所以



所以,


函数


所以满足条件的点


知识点
扫码查看完整答案与解析