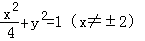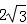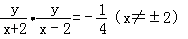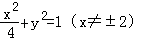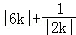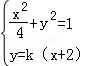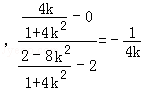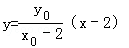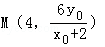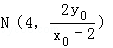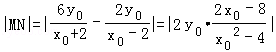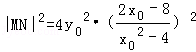- 椭圆的几何性质
- 共137题
已知动点P到点A（﹣2，0）与点B（2，0）的斜率之积为﹣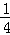
（1）求曲线C的方程；
（2）若点Q为曲线C上的一点，直线AQ，BQ与直线x=4分别交于M、N两点，直线BM与椭圆的交点为D，求线段MN长度的最小值。
正确答案
（1）
（2）
解析
（1）设P（x，y），由题意知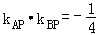 
化简得曲线C方程为：
（2）思路一
满足题意的直线AQ的斜率显然存在且不为零，设其方程为y=k（x+2），
由（Ⅰ）知
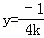
当x=4时得N点坐标为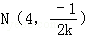
所以
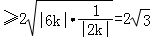
当且仅当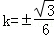
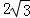
思路二：满足题意的直线AQ的斜率显然存在且不为零，设其方程为y=k（x+2），
联立方程：
消元得（4k2+1）x2+16k2x+16k2﹣4=0，
设Q（x0，y0），M（x1，y1），N（x2，y2），
由韦达定理得：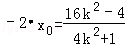
所以
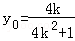
所以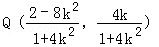
所以直线BQ的斜率为
以下同思路一
思路三：设Q（x0，y0），则直线AQ的方程为
直线BQ的方程为
当x=4，得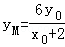
当x=4，得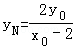
则
又
所以
利用导数，或变形为二次函数求其最小值。
知识点
A
B
C
D
正确答案
解析
略
知识点
已知P是以F1、F2为焦点的椭圆
A
B
C
D
正确答案
解析
由
∴
又知tan∠PF1F2 =
∴
而PF1 + PF2 = 2a，F1F2 = 2c
e =
知识点
设A1、A2为椭圆
点
A
B
C
D
正确答案
解析
略
知识点
已知焦点在
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析