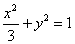- 椭圆的几何性质
- 共137题
已知椭圆



(1)求椭圆C的方程;
(2)对于椭圆C上任一点,若
正确答案
见解析。
解析
知识点
已知椭圆


(1)求椭圆
(2)











正确答案
见解析
解析
(1)由题意可知,


所以椭圆的方程为
(2)由(1)可知,



于是直线



即
又直线



即
所以
又



得


知识点
已知椭圆C:



(1)求椭圆C的离心率e;
(2)用m表示点E,F的坐标;
(3)证明直线EF与y轴交点的位置与m无关。
正确答案
见解析
解析
(1)依题意知


(2)








由


由


(3)据已知,




令x=0,得
知识点
已知椭圆







(1)求椭圆
(2)证明直线

正确答案
见解析
解析
(1)由题意知:
所以,焦点坐标为

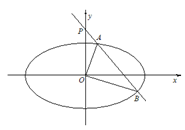
(2)由题意知:直线PB的斜率存在,设直线PB的方程为



由
则
直线AE的方程为


又


把(1)代入(3)式,整理得


知识点
已知椭圆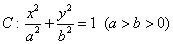
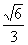
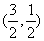
(1)求椭圆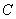
(2)过点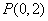
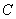
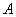
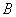
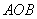
大值。
正确答案
(1)
(2)△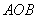
解析
(1)解: 由 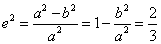
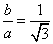
由椭圆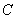
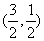
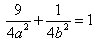
联立① ②,解得 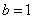
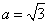
所以椭圆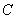
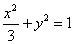
(2)解:易知直线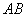
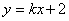
将直线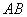
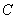
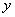
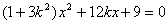
令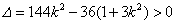
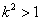
设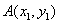
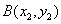
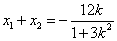
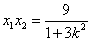
所以 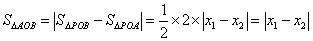
因为 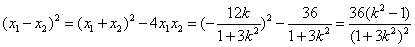
设 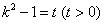
则 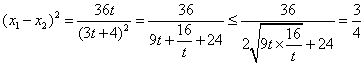
当且仅当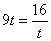
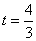
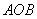
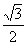
知识点
扫码查看完整答案与解析