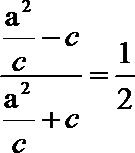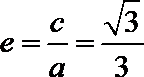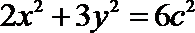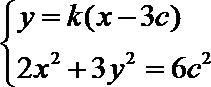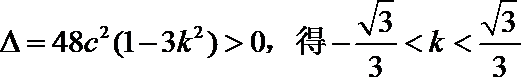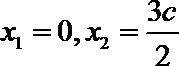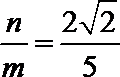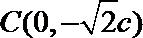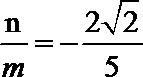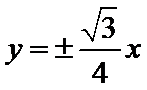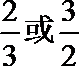- 椭圆的几何性质
- 共137题
4.椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知









正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆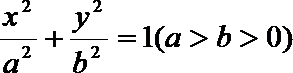
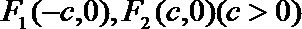
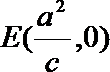
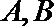
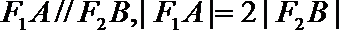
(1)求椭圆的离心率; 求直线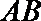
(2)设点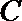
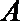
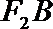
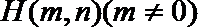
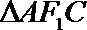

正确答案
解:(1)由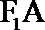
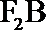
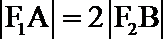
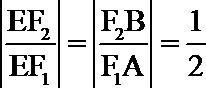
整理,得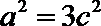
由(1)得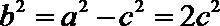
设直线AB的方程为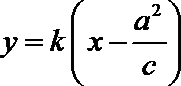
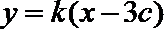
由已知设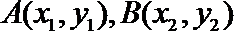
消去y整理,得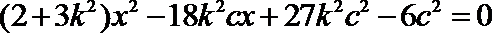
依题意,
而 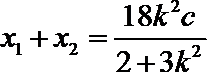
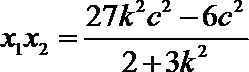
由题设知,点B为线段AE的中点,所以
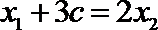
联立①③解得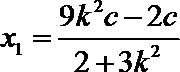
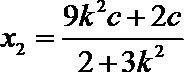
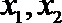
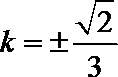
(2)解法一:可知
当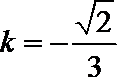
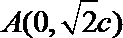
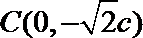
线段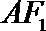
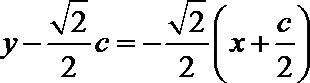
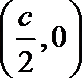
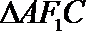
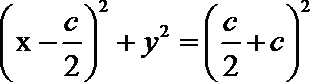
直线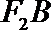
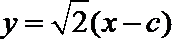
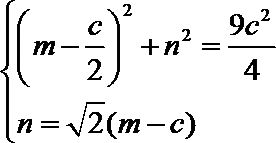
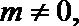
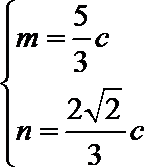
当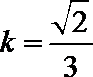
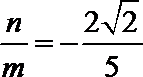
解法二:可知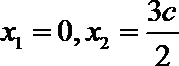
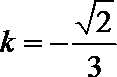
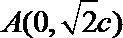
由椭圆的对称性可知B,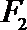
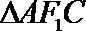
且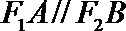
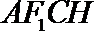
由直线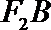
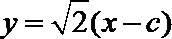
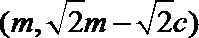
因为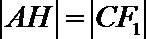
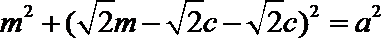
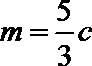
则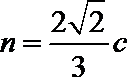
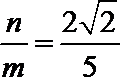
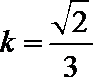
解析
解析已在路上飞奔,马上就到!
知识点
8. 如图,在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知椭圆的左焦点为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 设椭圆C:








(1)求椭圆
(2)若过

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知椭圆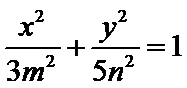
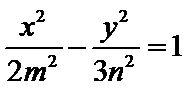
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知方程



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设圆锥曲线C的两个焦点分别为F1,F2,若曲线r上存在点P满足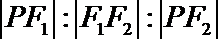
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析