椭圆的几何性质
共178题

· 椭圆的几何性质

椭圆的几何性质
共178题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

9.设F是椭圆的右焦点,且椭圆上至少有11个不同的点Pi(i=1,2,3,…),使,…组成公差为d的等差数列,则d的取值范围为　　　　.

正确答案

解析

若公差d>0,则|FP1|最小,

,数列中的最大项为

并设为第n项,

则

注意到d>0,得

若d<0,易得

那么d的取值范围为

知识点

等差数列的基本运算等差数列的性质及应用数列与解析几何的综合椭圆的几何性质

题型：填空题

填空题 · 5 分

8.已知椭圆C:+=1的左,右焦点分别为F1,F2,动直线l:y=x+m与椭圆C相切,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.则四边形F1MNF2的面积为 _______.

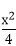
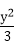
正确答案

解析

将直线l的方程y=x+m代入椭圆C的方程3x2+4y2=12中,得7x2+8mx+4m2-12=0.

由直线与椭圆C仅有一个公共点知,Δ=64m2-28(4m2-12)=0,化简得m2=7.

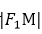
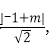
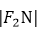
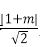
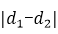
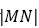
设d1==,d2==,又=,

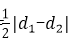
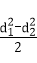
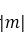
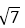
所以S=(d1+d2)=||==.

知识点

椭圆的几何性质直线与椭圆的位置关系

题型：单选题

单选题 · 5 分

5.过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1,P2,线段P1P2的中点为P。设直线l的斜率为k1(k1≠0)，直线OP(O为坐标原点)的斜率为k2,则k1k2等于（）

A-2

C-

正确答案

解析

设P1(x1,y1),P2(x2,y2),P(x0,y0),则,两式作差得,∴k1==-=-,又k2=,∴k1k2=-,故选C.

知识点

直线的倾斜角与斜率椭圆的几何性质直线与椭圆的位置关系圆锥曲线的定点、定值问题

题型：单选题

单选题 · 5 分

1．若双曲线的焦点在x轴上，则实数k的取值范围是（）

A（一∞，1）

B(2，+∞)

C(1,2)

D(一∞,1)U(2,+∞)

正确答案

解析

本题属于双曲线中的基本问题，题目的难度是简单。

考查方向

主要考查了双曲线的标准方程,在近几年的各省高考题出现的频率较高。

解题思路

无

易错点

本题易在求解时把分母平方运算。

知识点

椭圆的几何性质双曲线的几何性质

题型：简答题

简答题 · 13 分

20.已知椭圆C的中心在坐标原点O，左焦点为F(-l，0)，离心率为

（1）求椭圆C的标准方程；

（2）过点F的直线，与椭圆C交于A、B两点，设（其中1<入<3），求的取值范围。

正确答案

（1）；

（2）．

解析

本题属于圆锥曲线中的基本问题，题目的难度是逐渐由易到难，

（1）直接按照步骤来求

（2）要注意对参数的讨论．

（1）；

（2）由（其中1<入<3）知，直线l不水平，

设l：x=my-1,A(x1,y1),B(x2,y2)联立：

消x得：(2+m2)y2-2my-1=0,

得

①由（其中1<入<3）

得y1= -λy2……②

则，

令t=,则0<t<,

得……③。

=x1x2+y1y2=(my1-1)(my2-1)+y1y2=(1+m2)y1y2-m(y1+y2)+1=，

将③代入，得=，

从而∈。

考查方向

本题考查了椭圆的标准方程和直线与椭圆的位置关系、平面向量等知识点．

解题思路

无

易错点

1、第二问中的易丢对a的分类讨论。

知识点

椭圆的定义及标准方程椭圆的几何性质圆锥曲线中的范围、最值问题

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 椭圆的几何性质

扫码查看完整答案与解析