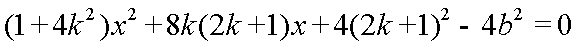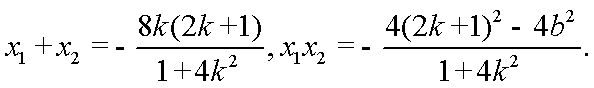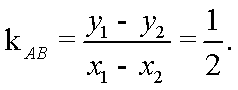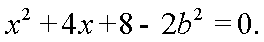- 椭圆的几何性质
- 共178题
如图,圆







23.求圆
24.过点


连接

正确答案
详见解析
解析
解:(Ⅰ)设圆



∵ 



∴ 圆


考查方向
求直线和圆的方程
解题思路
先求圆C的半径,然后带入方程中,求解参数
易错点
不能正确的设出坐标,找不到等量关系
正确答案
(Ⅱ)把



即点

(1)当

(2)当



联立方程



设直线



∴
若

∵
∴ 

考查方向
直线和圆的方程,直线和圆锥曲线的综合题
解题思路
设出直线AB的方程,联立方程,消去y,然后直线AN和直线BN的斜率的和等于0,证明角相等。
若椭圆





24.求椭圆的离心率;
25.过点





(2)【答案】设直线

∵


由(1)知,
由


∴

由①②知,
∵
∴
当且仅当



又当

∴由


正确答案
(1)由题意知,


解析
(1)由题意知,


考查方向
本题考查椭圆与抛物线的应用问题,主要涉及到两者焦距、焦点问题
解题思路
由题意,可知
易错点
线段的定比分点计算容易出错,离心率公式容易记错
教师点评
本题是椭圆焦距与抛物线焦点坐标的综合题,属于简单题,只要掌握线段定比分点的性质即可,在近几年中考到的频率较高,是解析几何中重要的一块
正确答案
直线方程为

椭圆方程为
解析
设直线

∵


由(1)知,
由


∴

由①②知,
∵
∴
当且仅当



又当

∴由


考查方向
本题考查椭圆中三角形面积最大问题,主要涉及到直线与椭圆的焦点问题、向量在椭圆中的应用问题以及函数值域问题
解题思路
先设出直线方程,联立椭圆方程和直线方程,利用韦达定理,求出两根和积,再利用向量坐标运算,求出关系式,列出面积公式,利用均值不等式求出直线方程和椭圆方程
易错点
计算容易出错,不容易想到均值不等式
教师点评
本题是向量、曲线相交与均值不等式的综合应用题,是一道难度较大的题型,需要掌握直线的不同设法、设而不求法、向量运算与面积问题、均值不等式在最值问题上会经常使用,值得注意
在平面直角坐标系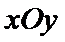
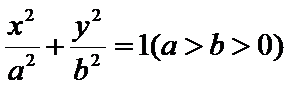
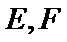
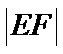
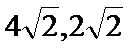
23.求椭圆的方程;
24.与圆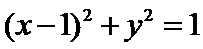
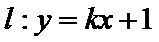
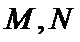
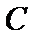
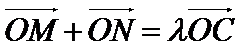
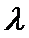
正确答案
(Ⅰ)由题意知,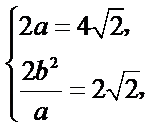
所求椭圆的方程为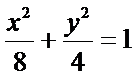

解析
由题意,得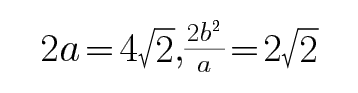
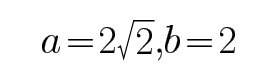
考查方向
本题考查椭圆焦点弦知识,由焦点弦的公式可以知道最大值与最小值
解题思路
由焦点弦公式,可得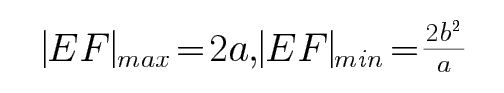
易错点
焦点弦的最大值与最小值容易弄错
教师点评
本题只需要记住焦点弦的公式就可以解决,在近几年中考到的频率较高,是解析几何中重要的一块
正确答案
(Ⅱ)设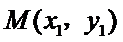
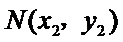
由直线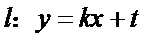
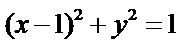
所以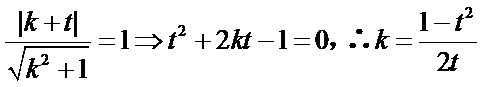
联立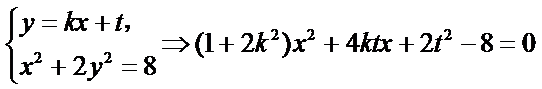
所以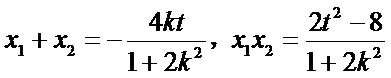
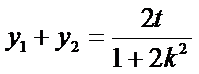
又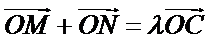
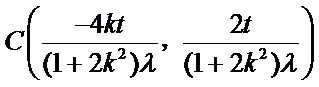
将点C代入椭圆方程并化简得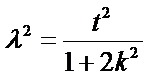
①代入②得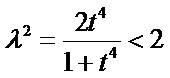
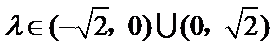
解析
(Ⅱ)设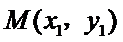
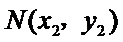
由直线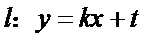
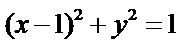
所以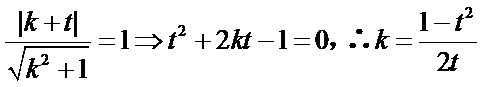
联立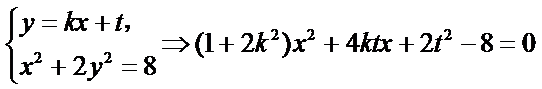
所以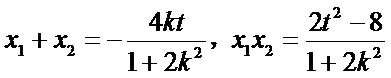
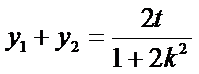
又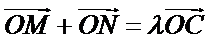
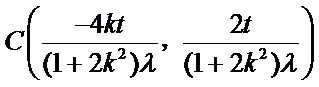
将点C代入椭圆方程并化简得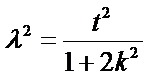
①代入②得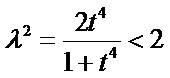
考查方向
本题考查圆与直线相切问题,向量在圆锥曲线上的应用,变量取值范围问题
解题思路
先由圆与直线相切,求出k,然后联立直线与椭圆方程,消去一个元,算出两根和积,再结合向量的性质,联立关系式,求出变量取值范围
易错点
容易算错斜率,以及变量的取值范围
教师点评
本题是圆锥曲线中的常规题,难度是中等,需要掌握切线问题、设而不求法、向量等知识,才能求出变量的取值范围,在近几年中考到的频率较高,是解析几何中重要的一块
20.已知椭圆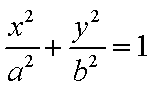
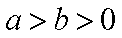


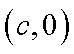
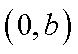
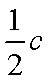
(1)求椭圆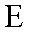
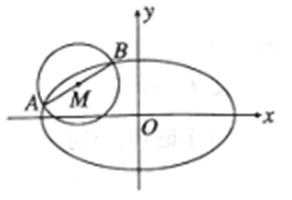
(2)如图,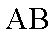
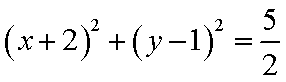
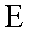
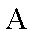
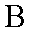
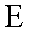
正确答案
(1)过点(c,0),(0,b)的直线方程为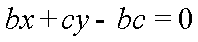
则原点O到直线的距离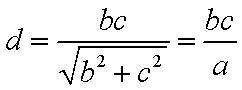
由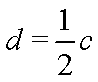
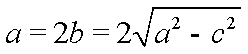
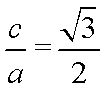
(2)解法一:由(1)知,椭圆E的方程为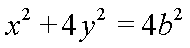
依题意,圆心M(-2,1)是线段AB的中点,且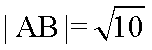
易知,AB不与x轴垂直,设其直线方程为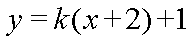
设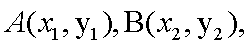
由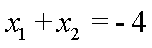
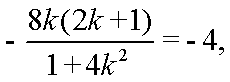
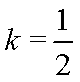
从而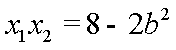
于是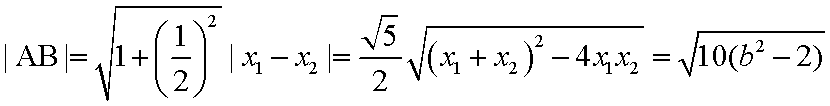
由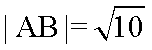
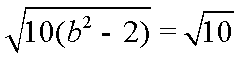
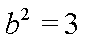
故椭圆E的方程为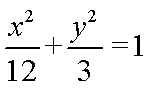
解法二:由(I)知,椭圆E的方程为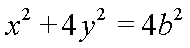
依题意,点A,B关于圆心M(-2,1)对称,且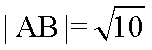
设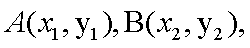
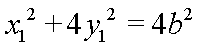
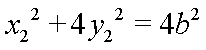
两式相减并结合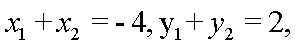
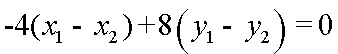
易知,AB不与x轴垂直,则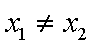
因此AB直线方程为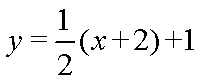
所以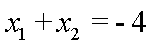
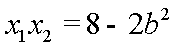
于是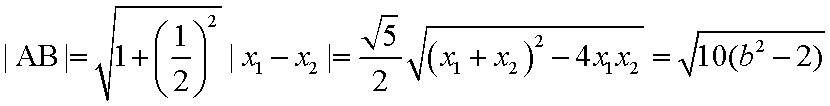
由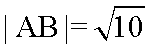
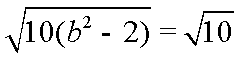
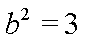
故椭圆E的方程为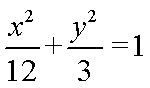
解析
解析已在路上飞奔,马上就到!
知识点
20.(本题满分12分)
已知椭圆








(Ⅰ)证明:直线

(Ⅱ)若






正确答案
(Ⅰ)详见解析;(Ⅱ)能,

试题分析:(Ⅰ)题中涉及弦的中点坐标问题,故可以采取“点差法”或“韦达定理”两种方法求解:设端点




(Ⅱ)根据(Ⅰ)中结论,设直线





试题(Ⅰ)设直线



将









(Ⅱ)四边形
因为直线





由(Ⅰ)得
























解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析