- 万有引力理论的成就
- 共70题
为了对火星及其周围的空间环境进行探测，我国预计于2011年10月发射第一颗火星探测器“萤火一号”。假设探测器在离火星表面高度分别为h1和h2的圆轨道上运动时，周期分别为T1和T2。火星可视为质量分布均匀的球体，且忽略火星的自转影响，万有引力常量为G。仅利用以上数据，可以计算出
A火星的密度和火星表面的重力加速度
B火星的质量和火星对“萤火一号”的引力
C火星的半径和“萤火一号”的质量
D火星表
正确答案
解析
由于万有引力提供探测器做圆周运动的向心力，则有
知识点
（1）开普勒行星运动第三定律指出：行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比，即
（2）开普勒定律不仅适用于太阳系，它对一切具有中心天体的引力系统（如地月系统）都成立。经测定月地距离为3.84×108m，月球绕地球运动的周期为2.36×106s，试计算地球的质M地。（G=6.67×10-11Nm2/kg2，结果保留一位有效数字）
正确答案
见解析。
解析
（1）因行星绕太阳作匀速圆周运动，于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有
（2）在月地系统中，设月球绕地球运动的轨道半径为R，周期为T，由（1）问可得
知识点
一卫星绕某一行星表面附近做匀速圆周运动，其线速度大小为
A
B
C
D
正确答案
解析
设星球半径为R，星球质量为M，卫星质量为m1,卫星做圆周运动向心力由万有引力提供即
知识点
设太阳质量为M，某行星绕太阳公转周期为T，轨道可视为r的圆。已知万有引力常量为G，则描述该行星运动的上述物理量满足
A
B
C
D
正确答案
解析
略
知识点
“嫦娥二号”是我国月球探测第二期工程的先导星。若测得“嫦娥二号”在月球（可视为密度均匀的球体）表面附近圆形轨道运行的周期T，已知引力常量为G，半径为R的球体体积公式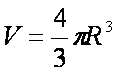
正确答案
解析
“嫦娥二号”在近月表面做周期已知的匀速圆周运动，有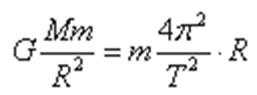
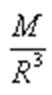
知识点
扫码查看完整答案与解析