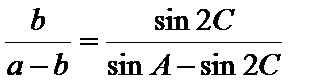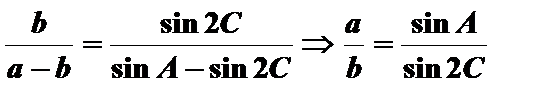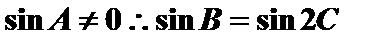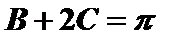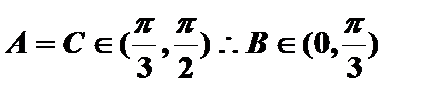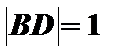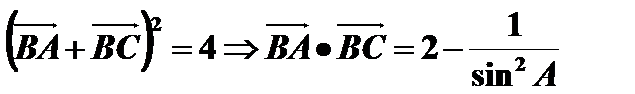- 正弦定理
- 共139题
1
题型:填空题
|
13.一艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是________海里.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理解三角形的实际应用
1
题型:
单选题
|
13.在


正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
充要条件的判定正弦定理
1
题型:简答题
|
17.在


(I) 求
(II) 求
正确答案
(Ⅰ)解:在△ABC中,根据正弦定理,
(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=
于是 sinA=

所以 sin(2A-


解析
解析已在路上飞奔,马上就到!
知识点
三角函数中的恒等变换应用正弦定理
1
题型:简答题
|
17.在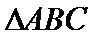
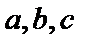
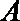
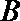
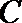
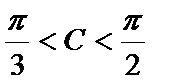
(1)判断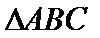
(2)若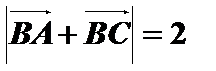
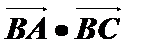
正确答案
解:(1)由题意
由正弦定理知,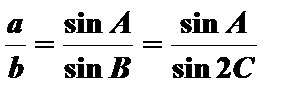
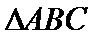
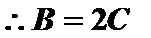
当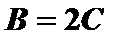
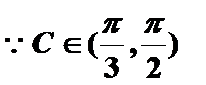
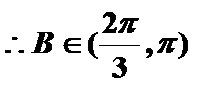

当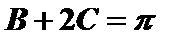
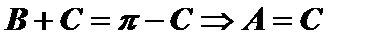
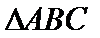
(2)在等腰三角形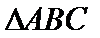
取AC中点D,由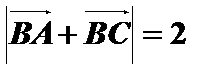
又由,
所以,
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理向量的模平面向量数量积的运算
1
题型:简答题
|
19.在不等边△ABC中,设A.B.C所对的边分别为a,b,c,已知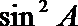
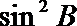
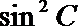
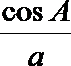
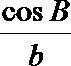
(1)试根据下列选项作出判断,并在括号内填上你认为是正确选项的代号( )
A.是等比数列而不是等差数列
B.是等差数列而不是等比数列
C.既是等比数列也是等差数列
D.既非等比数列也非等差数列
(2)证明你的判断
正确答案
(1)B
(2)因为

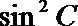
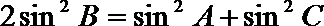
所以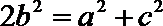
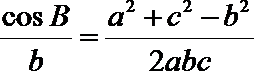

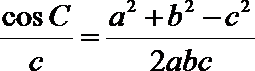
显然
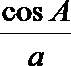
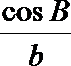
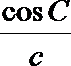
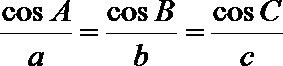

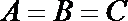
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理余弦定理等差数列的判断与证明等比数列的判断与证明
下一知识点 : 正弦定理的应用
扫码查看完整答案与解析