· 解三角形

· 正弦定理

正弦定理
共139题

· 解三角形

· 正弦定理

正弦定理
共139题

热门试卷

X 查看更多试卷

1

题型：单选题

|

单选题 · 5 分

9.在中，若，则的值为（）

A3

B4

C5

D6

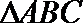
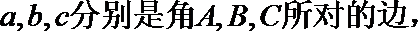
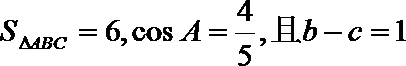
正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理

1

题型：简答题

|

简答题 · 14 分

14．（1）已知中，分别是角的对边，，则等于多少？

（2）在中，分别是角的对边，若，求边上的高是多少？

正确答案

（1）或；

（2）

解析

（1）由正弦定理：，

则：，

解得：

又由于是三角形中的角，

且由于，

于是：或

（2）由余弦定理：

，

所以

由面积公式，

解得：

知识点

正弦定理余弦定理三角形中的几何计算

1

题型：填空题

|

填空题 · 5 分

11．已知的三内角、、所对边长分别为是、、，设向量，，若∥，则角的大小为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用正弦定理平行向量与共线向量

1

题型：填空题

|

填空题 · 5 分

13．在中，内角A、B、C的对边长分别为a、b、c，已知，则（）．

正确答案

4

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理余弦定理

1

题型：简答题

|

简答题 · 13 分

15．已知函数，

（Ⅰ）求函数的最小正周期；

（Ⅱ）记的内角A,B,C的对边长分别为，若，求的值。

正确答案

（Ⅰ）

所以函数的最小正周期为。

（Ⅱ）由得,即

又因为,所以

所以,即.

因为

所以由正弦定理,得

故

当

当

故的值为1或2.

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用正弦定理余弦定理

继续学习学习下一知识点

下一知识点 : 正弦定理的应用

百度题库 > 高考 > 文科数学 > 正弦定理

扫码查看完整答案与解析