- 平抛运动
- 共223题
水上滑梯可简化成如图所示的模型,斜槽AB和水平槽BC平滑连接,斜槽AB的竖直高度H=5.0m,倾角θ=37°。BC面与水面的距离h=0.80m,人与AB、BC间的摩擦均忽略不计。取重力加速度g=10m/s2,cos37°=0.8,sin37°=0.6。一同学从滑梯顶端A点无初速地自由滑下,
求:
(1)该同学沿斜槽AB下滑时加速度的大小a;
(2)该同学滑到B点时速度的大小vB;
(3)从C点滑出至落到水面的过程中,该同学在水平方向位移的大小x。
正确答案
见解析。
解析
(1)该同学沿斜槽AB下滑过程中,受重力和斜槽的支持力,由牛顿第二定律
可得 a=6m/s2
(2)由A到B的过程中只有重力做功,设到达B点时速度为 vB ,由机械能守恒定律
可得 vB =10m/s
(3)由B到C该同学做匀速直线运动,到达C点时的速度为 vC =vB=10m/s ,由C点到落入水面做平抛运动,有
水平方向
竖直方向
可得 x=4m
知识点
以初速为

正确答案
解析
略
知识点
如图所示,为供儿童娱乐的滑梯的示意图,其中AB为斜面滑槽,与水平方向的夹角为θ=37°;长L的BC水平滑槽,与半径R=0.2m的
(取g=10 m/s2,sin370=0.6, cos370=0.8)试求:
(1)儿童在斜面滑槽上滑下时的加速度大小?
(2)为了使儿童在娱乐时不会从C处平抛滑出,水平滑槽BC的长度L至少为多少?
正确答案
(1)2 m/s2
(2)L≥1 m
解析
(1)设儿童下滑的加速度大小为a,则有
mgsin37°-μmgcos37°=ma1
解得:a1=2 m/s2.
(2)因为H=2 m,圆弧CD的半径R=0.8 m,
所以AB的长度
设儿童滑到B点的速率为vB,则:vB2=2aL1,
(或依动能定理: 
由②③④解得:
设儿童在C点恰做平抛运动滑出时的速率为vC,则:
f=umg=ma2
-2a2L≤vC2-vB 2
(或用动能定理:
解得:L≥1 m.
知识点
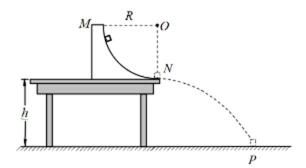
如图所示,半径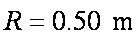
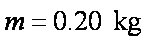
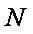
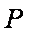
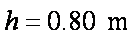


求:
(1)圆轨道上释放小物块的位置与桌面间的高度差;
(2)小物块经过
(3)小物块落地前瞬间的动量大小。
正确答案
见解析。
解析
(1)设圆轨道上释放小物块的位置与桌面间的高度差为H,小物块运动至N点过程中机械能守恒,则有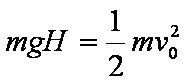
解得 H=0.45m
(2)设物块经过N点时所受支持力为F
根据牛顿第二定律有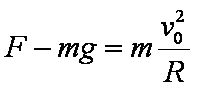
解得 F=5.6 N
(3)设物块做平抛运动的时间为t,小物块落地前竖直分速度为vy,
则 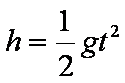
vy=gt
解得 vy=4.0m/s
小物块落地前速度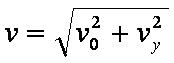
解得v=5.0m/s
动量p=mv
p=1.0kg·m/s
知识点
如图所示为利用电磁作用输送非导电液体装置的示意图。一边长为L、截面为正方形的塑料管道水平放置,其右端面上有一截面积为S的小喷口,喷口离地的高度为h,管道中有一绝缘活塞,在活塞的中部嵌有金属棒,整个装置放在竖直向上的匀强磁场中,当棒中通有垂直纸面向里的恒定电流I时,活塞以某一速度向右匀速推动液体,液体以不变的速度v源源不断地沿水平方向射出。若液体的密度为ρ,重力加速度为g,不计所有阻力。
求
(1)液体落地点离喷口的水平距离x;
(2)该装置的功率;
(3)磁感应强度B的大小。
正确答案
见解析。
解析
(1)液体喷出后做平抛运动


解得:
(2)设活塞运动速度v0
由 
得
设在时间t内有质量为△m的液体从喷口射出

时间t内装置对△m做功


(3)金属棒在磁场中受力

得
知识点
自然界中某个量




正确答案
解析
略
知识点
如图所示,一固定的1/4圆弧轨道,半径为1.25m,表面光滑,其底端与水平面相切,且与水平面右端P点相距6m。轨道的下方有一长为l.5m的薄木板,木板右侧与轨道右侧相齐。现让质量为lkg的物块从轨道的顶端由静止滑下,当物块滑到轨道底端时,木板从轨道下方的缝隙中冲出,此后木板在水平推力的作用下保持6m/s的速度匀速运动,物块则在木板上滑动。当木板右侧到达P点时,立即停止运动并被锁定,物块则继续运动,最终落到地面上。已知P点与地面相距1.75m,物块与木板间的动摩擦因数为0.1,取重力加速度g=10m/s2,不计木板的厚度和缝隙大小,求:(结果保留两位有效数字)
(1)物块滑到弧形轨道底端受到的支持力大小;
(2)物块离开木板时的速度大小;
(3)物块落地时的速度大小及落地点与P点的水平距离。
正确答案
(1)30N
(2)
(3)3.5m
解析
(1)对物块
解得
(2)木板运动时间
对物块

(3)由机械能守恒定律得
物块在竖直方向
物块在水平方向
知识点
A、B两质点以相同的水平速度υ0抛出,A在竖直平面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2,不计阻力,如图所示,比较P1、P2在x轴上的远近关系是 ( )
正确答案
解析
略
知识点
如图所示,一质量m=0.1kg、电量q=1.0×10-5 C的带正电小球(可视作点电荷),它在一高度和水平位置都可以调节的平台上滑行一段距离后平抛,并沿圆弧轨道下滑。A、B为圆弧两端点,其连线水平,已知圆弧半径R=1.0m,平台距AB连线的高度h可以在0.2m-0.8m.之间调节。有一平行半径OA方向的匀强电场E,只存在圆弧区域内。为保证小球从不同高度h平抛,都恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,小球平抛初速度v0和h满足如图所示的抛物线,同时调节平台离开A点的距离合适。不计空气阻力,取g=10m/s2,求:
(1)小球在空中飞行的最短时间t;
(2)平台离开A的水平距离x范围;
(3)当h=0.2m且E=2.5×104N/C时,小球滑到最低点C点的速度v;
(4)为了保证小球在圆轨道内滑动到C点的速度都是(3)中的v,则电场力F=qE的大小应与平台高度h满足的关系。(通过列式运算说明)
正确答案
(1)当平台高度为0.2m时,空中飞行的最短时间t=
(2)因为小球从不同高度h平抛,都恰能无碰撞地沿圆弧切线从A点进入光滑竖直圆弧轨道,所以小球进入圆弧轨道时时的速度方向不变,设此速度与竖直方向成α角。
tgα=
v02=2ghtan2α
由图像中当h=0.8m时,v0=3m/s代入上式得
9=2×10×0.8×tg2α
tgα=0.75 α=370 则θ=1060
所以v02=11.25h
当h=0.2m时, v0=1.5m/s
平台离开A的最小距离为s1= v0t=1.5×0.2=0.3m
同理得平台离开A的最大距离为s2= v0

(3)小球到达A点时的速度vA=

从A点到C点,由动能定理得
mgR(1-cos530)-qE R(1-cos530)= 

代入数据,解得vC=3.5m/s
(4)从A点到C点,由动能定理得
mgR(1-cos530)-FR(1-cos530)=

=

=

代入数据得32F=125h-17
或
解析
略
知识点
做平抛运动的物体,每秒的速度增量总是( )
正确答案
解析
略
知识点
扫码查看完整答案与解析