- 函数概念与表示
- 共1891题
近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5,为了保证正常用电,安装后采用太阳能和电能互补供电的模式,假设在此模式下,安装后该企业每年消耗的电费C(单位:万元)与安装的这种太阳能电池板的面积x(单位:平方米)之间的函数关系是C(x)=
(1)试解释C(0)的实际意义,并建立F关于x的函数关系式;
(2)当x为多少平方米时,F取得最小值?最小值是多少万元?
正确答案
见解析
解析
(1)C(0)的实际意义是安装这种太阳能电池板的面积为0时的用电费用,
即未安装电阳能供电设备时全村每年消耗的电费
由C(0)=
所以F=15×

(2)因为

当且仅当
所以当x为55平方米时,F取得最小值为57.5万元
知识点
对于定义在区间D上的函数f(x),若任给x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭。
(1)试判断f(x)=x﹣1在区间[﹣2.1]上是否封闭,并说明理由;
(2)若函数g(x)=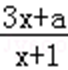
(3)若函数h(x)=x3﹣3x在区间[a,b[(a,b∈Z)上封闭,求a,b的值。
正确答案
故答案为:0.8
解析
(1)f(x)=x﹣1在区间[﹣2,1]上单调递增,所以f(x)的值域为[﹣3,0]
而[﹣3,0]⊈[﹣2,1],所以f(x)在区间[﹣2,1]上不是封闭的;
(2)因为g(x)=
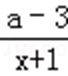
①当a=3时,函数g(x)的值域为{3}⊆[3,10],适合题意。
②当a>3时,函数g(x)=3+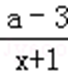

由

③当a<3时,在区间[3,10]上有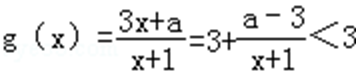
综上所述,实数a的取值范围是3≤a≤31;
(3)因为h(x)=x3﹣3x,所以h′(x)=3x2﹣3=3(x+1)(x﹣1),
当x∈(﹣∞,﹣1)时,h′(x)>0,当x∈(﹣1,1)时,h′(x)0。
所以h(x)在(﹣∞,﹣1)上单调递增,在(﹣1,1)上递减,在(1,+∞)上递增。
①当a<b≤﹣1时,h(x)在区间[a,b]上递增,所以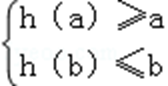
即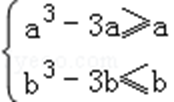
②当a≤﹣1且﹣1<b≤1时,因h(x)max=h(﹣1)=2>b,矛盾,不合题意
③当a≤﹣1且b>1时,因为h(﹣1)=2,h(1)=﹣2都在函数的值域内,故a≤﹣2,b≥2,
又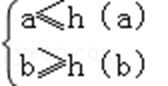

④当﹣1≤a<b≤1时,h(x)在区间[a,b]上递减,
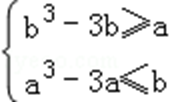
而a,b∈Z,经检验,满足﹣1≤a<b≤1的整数组a,b均不合(*)式。
⑤当﹣1<a<1且b≥1时,因h(x)min=h(1)=﹣2<a,矛盾,不合题意。
⑥当b>a≥1时,h(x)在区间[a,b]上递增,所以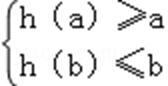
即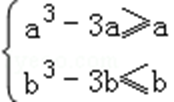
综上所述,所求整数a,b的值为a=﹣2,b=2
知识点
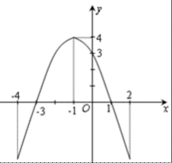
如图是一个二次函数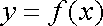
(1)写出这个二次函数的零点;
(2)写出这个二次函数的解析式及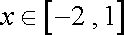
正确答案
见解析。
解析
(1)由图可知这个二次函数的零点为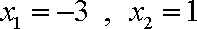
(2)可设两点式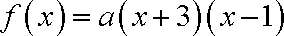
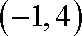
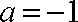
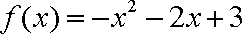
其在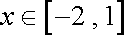
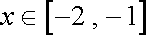
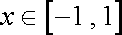

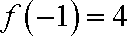
又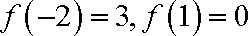


知识点
某加工厂需要定期购买原材料,已知每公斤材料的价格为1.5元,每次购买原材料需支付运费600元,每公斤原材料每天的保管费用为0.03元,该厂每天需要消耗原材料400公斤,每次购买的原材料当天即开始使用(即有400公斤不需要保管)。
(1)设该厂每



(2)求该厂多少天购买一次原材料才能使平均每天支付的总费用
正确答案
见解析。
解析
(1)每次购买的原材料在x天内总的保管费用

(2)由(2)可知购买一次原材料的总的费用为
所以购买一次原材料平均每天支付的总费用
∴


∴该厂10天购买一次原材料可以使平均每天支付的总费用y最少,为714元,……12分
知识点
济南高新区引进一高科技企业,投入资金720万元建设基本设施,第一年各种运营费用120万元,以后每年增加40万元;每年企业销售收入500万元,设




(1)从第几年开始获取纯利润?
(2)若干年后,该企业为开发新产品,有两种处理方案:
①年平均利润最大时,以480万元出售该企业;
②纯利润最大时,以160万元出售该企业;
问哪种方案最合算?
正确答案
见解析。
解析
由题意知每年的运营费用是以120为首项,40为公差的等差数列.设纯利润与年数的关系为
设
(1)获取纯利润就是要求



(2)①年平均利润



②


故此方案共获利1280+160=1440(万元). -----------------9分
比较两种方案,在同等数额获利的基础上,第①种方案只需6年,第②种方案需要10年,故选择第①种方案. 
知识点
已知函数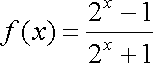
(1)判断函数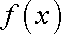
(2)求证: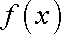
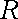
正确答案
见解析。
解析
(1)函数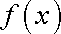
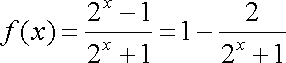
所以
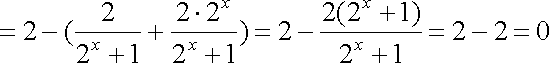
即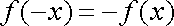
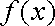
(2)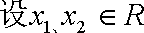

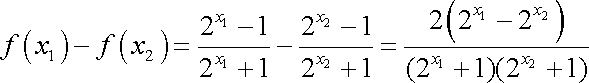

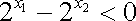

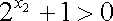
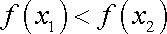
所以,函数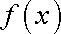
知识点
已知函数
(1)若函数y=f(x)的图像关于直线
(2)若存在

正确答案
(1)a=
解析
19. 解析:(1)
…………………………………………………………2分

又

(2)

则
知识点
已知向量
(1)当

(2)设函数




正确答案
(1)
解析
解析:(1)

(2)
由正弦定理得

因为



所以 
知识点
设函数
(1)求函数
(2)当

(3)关于x的方程
正确答案
见解析
解析
解析:(1)由



由





(2)由(1)知,f(x)在


又




即




(3)由
令
由









知识点
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度




(1)当

(2)当车流密度

正确答案
见解析。
解析
(1)由题意,当


由已知

故函数

(2)由题意并由(1)可得
当



当
当且仅当

所以当



综上可知,当


即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时---12分
知识点
扫码查看完整答案与解析