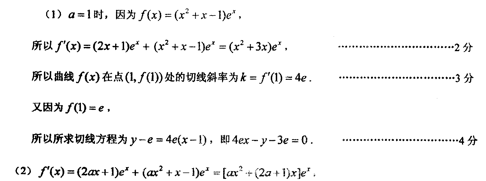函数的基本性质
共1471题

函数的基本性质
共1471题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知函数的最小正周期为，则的单调递增区间

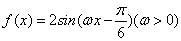
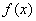
正确答案

解析

略

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 12 分

已知函数.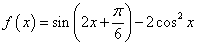

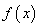
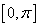
（1）求函数在上的单调递减区间；

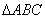
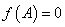
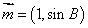
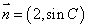
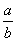
（2）设的内角A,B,C的对应边分别为a，b，c，且，若向量与向量共线，求的值.

正确答案

见解析。

解析

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 14 分

已知函数，其中e是自然对数的底数，

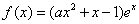
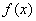
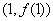
（1）若a=l，求曲线在点）处的切线方程；

（2）若a<0，求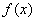的单调区间；

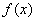
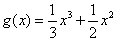
（3）若a=－1，函数的图象与函数的图象有3个不同的交点，求实数m的取值范围。

正确答案

见解析。

解析

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 12 分

已知是偶函数。

（1）求实常数的值，并给出函数的单调区间（不要求证明）；

（2）为实常数，解关于的不等式：。

正确答案

见解析。

解析

（1）是偶函数, 。

对一切恒成立,，

,的递增区间为，递减区间为，

（2）是偶函数 ,,

不等式即,由于在上是增函数,

, ,

即,,

时，不等式解集为；

时，不等式解集为，

知识点

函数的单调性及单调区间函数奇偶性的性质其它不等式的解法

题型：简答题

简答题 · 13 分

已知函数。

（1）判断的单调性；

（2）求函数的零点的个数；

（3）令，若函数在(0，)内有极值，求实数a的取值范围；

正确答案

见解析。

解析

知识点

函数的单调性及单调区间函数零点的判断和求解利用导数求函数的极值

题型：简答题

简答题 · 12 分

已知函数

（1）求f(x)的最小正周期和最小值；

（2）已知，求证：[f(β)]2－2＝0。

正确答案

见解析。

解析

(1)

∴T＝2π，f(x)的最小值为－2.

(2)证明：

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 13 分

已知函数，，其中。

（1）求的极值；

（2）若存在区间，使和在区间上具有相同的单调性，求的取值范围。

正确答案

（1）的极小值为；没有极大值

（2）的取值范围是

解析

（1）解：的定义域为，且。 ……………2分

① 当时，，故在上单调递增，从而没有极大值，也没有极小值。 …………4分

② 当时，令，得，

和的情况如下：

故的单调减区间为；单调增区间为。

从而的极小值为；没有极大值。 ………………6分

（2）解：的定义域为，且。 ………………8分

③ 当时，在上单调递增，在上单调递减，不合题意。…………9分

④ 当时，，在上单调递减。

当时，，此时在上单调递增，由于在上单调递减，不合题意。 ……11分

当时，，此时在上单调递减，由于在上单调递减，符合题意。

综上，的取值范围是。 ………13分

知识点

函数的单调性及单调区间

题型：单选题

单选题 · 5 分

已知实数满足约束条件若函数的最大值为1，则的最小值为

正确答案

解析

略

知识点

函数的单调性及单调区间

题型：简答题

简答题 · 12 分

已知函数

（1）求的单调递增区间；

（2）已知.

正确答案

见解析。

解析

知识点

函数的单调性及单调区间

题型：单选题

单选题 · 5 分

下列函数中，在上单调递减，并且是偶函数的是

正确答案

解析

四个函数中，是偶函数的有，又在内单调递增，故选。

知识点

函数的单调性及单调区间

继续学习学习下一知识点

下一知识点 : 二次函数与幂函数

百度题库 > 高考 > 文科数学 > 函数的基本性质

扫码查看完整答案与解析