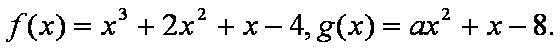- 函数概念与表示
- 共1891题
已知函数
(1)求函数
(2)求函数
正确答案
见解析
解析
(1)因为f(x)=

所以函数f(x)的最小正周期为2π
(2)令
得
故函数f(x)的单调增区间为[2kπ-

知识点
已知函数



(1)求
(2)求函数
(3)0设函数

正确答案
见解析
解析
(1)设
则:



(2)

所以



(3)

若函数



即



则

所以函数


知识点
已知函数
(1)若函数


(2)若函数


(3)在(1)的条件下,判断过点

正确答案
见解析
解析
(1)
∵ 


∴ 


∴ 

∴ 
(2)若函数

则
∴ 

∴ 
(3)

则


∴ 切线的斜率为

设
由


∴


∴ 函数


∵ 

∴ 方程
∴ 过点

知识点
已知



(1)当


(2)求函数

(3)若在区间



正确答案
见解析。
解析
由

(1)当

所以

(2)令
(1) 当

故


(2)当


所以

(3)设
对

因为





依题意,只需

即

所以正实数

知识点
设函数


(1)若直线




(2)若函数

正确答案
见解析。
解析
(1)由


由


(i)当
(ii)当



(2)
(i)若函数








(ii)若函数








综上可得,若函数


知识点
已知函数
(1)求函数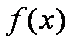
(2)若对任意的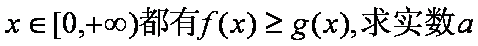
正确答案
见解析
解析
解:(1)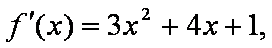
令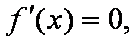
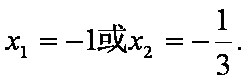
当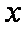
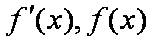
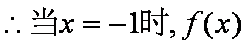

(2)设
若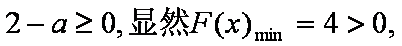
若
令
当
当
即
解不等式得:
当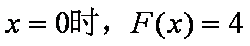
综上所述
知识点
函数




正确答案
解析
当










当









综上所述,
知识点
已知函数

(1)若函数



(2)当

正确答案
见解析
解析
(1)函数




(2)令

若


若

∴当



∴


∴
又∵

∴
∴

综上,当

知识点
设变量x、y满足约束条件
正确答案
解析
设变量x、y满足约束条件
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),
则目标函数z=2x+y的最小值为3。
知识点
已知函数f(x)=x3﹣tx2+3x,若对于任意的a∈[1,2],b﹣a=1,函数f(x)在区间(a,b)上单调递减,则实数t的取值范围是( )
正确答案
解析
f′(x)=3x2﹣2tx+3,
因为f(x)在区间(a,b)上单调递减,
所以f′(x)≤0即3x2﹣2tx+3≤0在(a,b)上恒成立,
所以有

所以
因为对于任意的a∈[1,2],f(x)在(a,b)上单调递减,所以(*)式恒成立,
又

所以
知识点
扫码查看完整答案与解析