- 函数概念与表示
- 共1891题
设函数







(1)写出
(2)设点



(3)设

正确答案
(1)函数


解析
解析:(1)、因为函数

所以
函数

(2)设

直线

则

联立

(3)


∴

∴ 

当且仅当
∴


知识点
已知函数
(1)求函数


(2)用定义证明函数

(3)如果当




正确答案
见解析
解析
解析:(1)令


对任意
所以函数
另证:对任意
所以函数
(2)设

∴
∴
∴


∴
所以函数

(3)由(2)知,函数

又因为


所以



故






所以
知识点
已知二次函数




(1)求
(2)若

(3)若曲线


正确答案
见解析。
解析
(1)设

∴

∴
∵
∴
∴
(2)∵
∴
令
∴
∴
∴
∵
①当


∴
②
③当


所以
(3)
∵
∴
∵

由题意得
∴
∴
知识点
已知函数
(1)若a=1,求g(x)的单调减区间;
(2)当a∈(0,+∞)时,若存在一个与a有关的负数M,使得对任意x∈[M,0]时,﹣4≤f(x)≤4恒成立,求M的最小值及相应的a值。
正确答案
见解析
解析
(1)当a=1时,
由g'(x)<0解得
∴当a=1时函数g(x)的单调减区间为
(2)易知
显然f(0)=﹣2,由(2)知抛物线的对称轴
①当

此时M取较大的根,即
∵0<a<2,∴
②当

令ax2+4x﹣2=4解得
此时M取较小的根,即
∵a≥2,∴
由于﹣3<﹣1,所以当a=2时,M取得最小值﹣3
知识点
已知函数
(1)求


正确答案
见解析
解析
(1)解:


(2)解法1:因为

所以

因为
由①、②解得
所以

解法2:因为

所以

知识点
已知





(1)求
(2)若方程

(3)设





正确答案
(1)
(2)
解析
解析:(1)由



(2)









(3)因为



所以

知识点
设x=1是函数
(1) 求a的值,并求函数f(x)的单调区间;
(2)若函数f(x)在闭区间[m,m+1]上的最小值为0,最大值为
正确答案
见解析。
解析
(1)
由已知有:f'(1)=0,
从而
令f'(x)=0得:x1=1,
当x变化时,f'(x)、f(x)的变化情况如下表:
从上表可知:f(x)在
在
(2)由(1)知:
∵m>-1
①当-1<m<0时,0<m+1<1,f(x)在闭区间[m,m+1]上是增函数。
∴ f(m)=0,即

∴此时m不存在
②当0≤m<1时,m+1∈[1,2),此时最大值为
又f(x)的最小值为f(m)=0,
③当m≥1时,f(x)在闭区间[m,m+1]上是减函数。
知识点
已知函数
(1)求函数
(2)求函数

正确答案
(1)
解析
解析:(1)
所以函数

(2)
∵



∴
另解:
∵


∴

知识点
如图,在平面四边形ABCD中,AB=AD=2,
(1)将四边形ABCD的面积

(2)求

正确答案
见解析。
解析
(1)在△ABC中由余弦定理得


∵

∴四形ABCD的面积
(2)∵

∴当

知识点
已知函数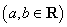
(1)求函数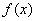
(2)若对任意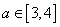
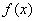
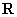
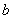
正确答案
见解析
解析
(1)解:因为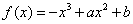
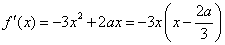
当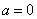
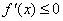
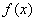
当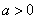
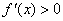
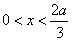
故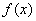
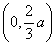
当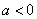
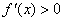
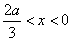
故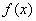
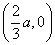
综上所述,当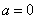
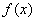
当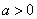
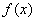
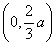
当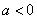
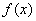
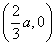
(2)解:,由(1)知,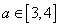
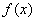
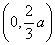
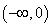
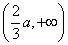
所以函数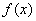
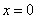
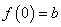
函数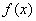
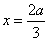
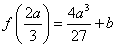
由于对任意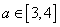
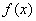
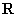
所以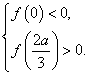
解得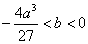
因为对任意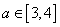
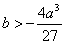

所以实数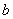
知识点
扫码查看完整答案与解析