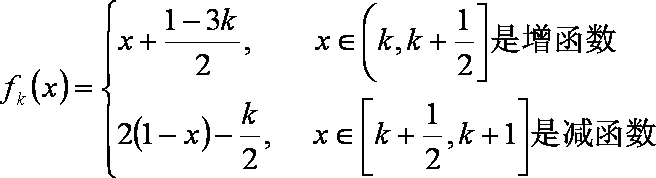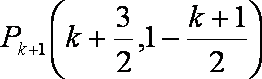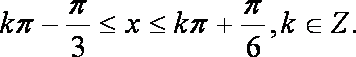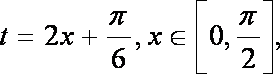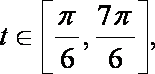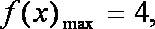- 指数函数的单调性与特殊点
- 共175题
已知函数



正确答案
-5;
解析
略
知识点
设各项均为正数的数列



(1)若λ = 1,求数列
(2)求λ的值,使数列
正确答案
见解析。
解析
(1)若λ = 1,则

又∵

∴
化简,得
∴当

由② ①,得


∵当n = 1时, 
∴数列{an}是首项为1,公比为2的等比数列, an = 2n1(
(2)令n = 1,得

要使数列

当λ = 0时,

当n≥2时,
整理,得

从而
化简,得

综上所述,

所以λ = 0时,数列
知识点
已知函数
(1)讨论函数
(2)设
数的底数),
正确答案
见解析
解析
(1)因为
所以
①若



②若




当



③若




当



综上:①当


②当




③当




(2)当

由(1)知,若



当


所以
因为对任意的

问题等价于对于任意

即

即

因为函数


所以函数


所以

知识点
函数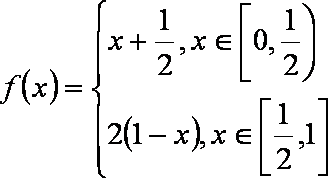
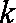
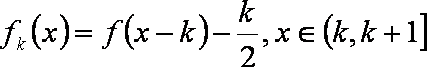
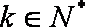
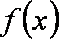
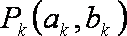
(1)直接写出不等式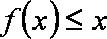
(2)求证:所有的点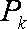
正确答案
见解析
解析
(1)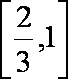
(2)∵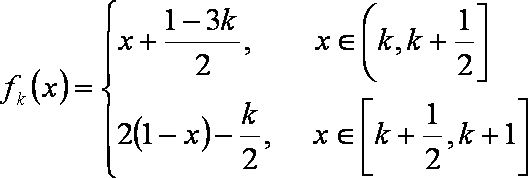
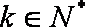
∴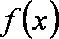
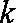
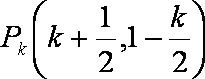
第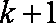
所以过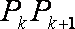
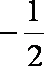
同理可得过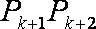
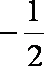
所以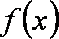

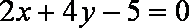
知识点
已知函数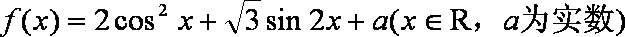
(1)求f(x)的周期和单调递增区间;
(2)若x∈[0,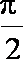
正确答案
见解析。
解析
(1)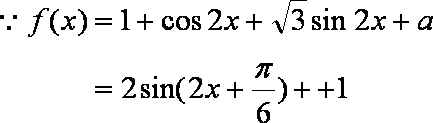
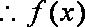
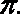
由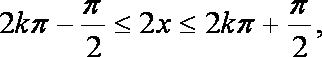
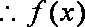
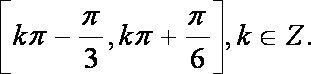
(2)令
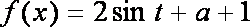

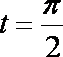
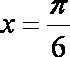
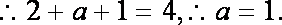
知识点
扫码查看完整答案与解析