- 平行关系的综合应用
- 共147题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设等差数列{an}的公差为d,点(an,bn)在函数f(x)=2x的图象上(n∈N*)。
(1)证明:数列{bn}为等比数列;
(2)若a1=1,函数f(x)的图象在点(a2,b2)处的切线在x轴上的截距为

正确答案
见解析
解析
(1)证明:由已知,bn=
当n≥1时,
所以,数列{bn}是首项为
(2)函数f(x)=2x在(a2,b2)处的切线方程为y-

它在x轴上的截距为
由题意,
解得a2=2.
所以,d=a2-a1=1,an=n,bn=2n,
于是,Tn=1×4+2×42+3×43+…+(n-1)·4n-1+n·4n,
4Tn=1×42+2×43+…+(n-1)×4n+n·4n+1.
因此,Tn-4Tn=4+42+…+4n-n·4n+1

所以,
知识点
某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率;
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率。
正确答案
(1)0.27
(2)0.24
解析
(1)设A表示事件“赔付金额为3000元,”B表示事件“赔付金额为4000元”,以频率估计概率得
P(A)=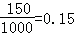
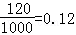
由于投保额为2800元,赔付金额大于投保金额得情形是3000元和4000元,所以其概率为P(A)+P(B)=0.15+0.12=0.27。
(2)设C表示事件“投保车辆中新司机获赔4000元”,由已知,样本车辆中车主为新司机的有0.1×1000=100,而赔付金额为4000元的车辆中车主为新司机的有0.2×120=24,
所以样本中车辆中新司机车主获赔金额为4000元的频率为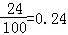
由频率估计概率得P(C)=0.24。
知识点
设复数z满足(z﹣2i)(2﹣i)=5,则z=( )
正确答案
解析
由(z﹣2i)(2﹣i)=5,得:

∴z=2+3i。
知识点
已知点A(﹣2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
正确答案
解析
∵点A(﹣2,3)在抛物线C:y2=2px的准线上,
∴
∴F(2,0),
∴直线AF的斜率为

知识点
有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5,39.5) 7 [39.5,43.5) 3
根据样本的频率分布估计,大于或等于31.5的数据约占
正确答案
解析
大于或等于31.5的数据共有12+7+3=22个,约占
知识点
设a,b,m,n∈R,且a2+b2=5,ma+nb=5,则
正确答案
解析
由柯西不等式得,
(ma+nb)2≤(m2+n2)(a2+b2)
∵a2+b2=5,ma+nb=5,
∴(m2+n2)≥5
∴
故答案为:
知识点
已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
正确答案
解析
A)若m∥α,n∥α,则m,n相交或平行或异面,故A错;
B)若m⊥α,n⊂α,则m⊥n,故B正确;
C)若m⊥α,m⊥n,则n∥α或n⊂α,故C错;
D)若m∥α,m⊥n,则n∥α或n⊂α或n⊥α,故D错。
知识点
设等差数列{an}的公差为d,若数列{2
正确答案
解析
∵数列{2
∴

∴
∴a1(an+1﹣an)=a1d<0
知识点
扫码查看完整答案与解析