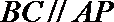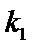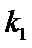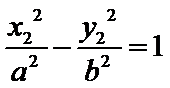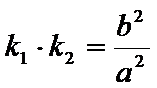- 平行关系的综合应用
- 共147题
9.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知实数x,y满足不等式组


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
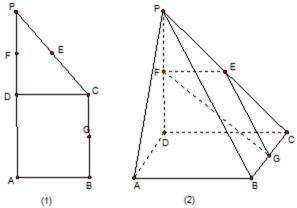
19.如图(1)在直角梯形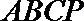
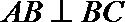
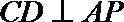
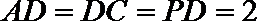
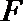
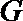
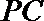
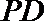
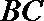
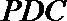
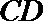
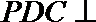
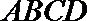
(1)求二面角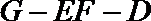
(2)在线段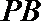
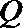
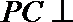
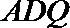
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,直角梯形ACDE与等腰直角

(1)求证:平面BCD⊥平面ABC
(2)求证:AF//平面BDE
(3)求四面体B-CDE的体积
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.下列命题中:
(1)平行于同一直线的两个平面平行;
(2)平行于同一平面的两个平面平行;
(3)垂直于同一直线的两直线平行;
(4)垂直于同一平面的两直线
其中所有正确的命题有_____________。
正确答案
(2)(4)
解析
解析已在路上飞奔,马上就到!
知识点
19.已知梯形














(1)当

(2)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(﹣2)= _________ .
正确答案
﹣1
解析
解析已在路上飞奔,马上就到!
知识点
22.设斜率为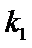
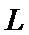
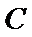
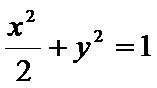
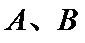
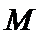
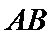
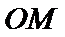
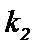
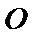
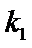
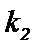
(1)求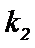
(2)把上述椭圆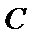
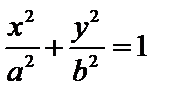
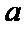
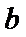
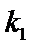
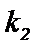
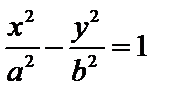
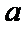
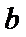
正确答案
(2)对于椭圆,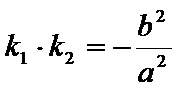
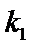
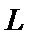
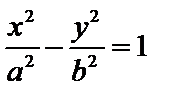
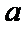
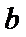
于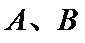
点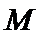
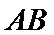
直线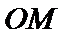
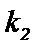
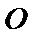
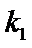
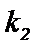
则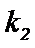
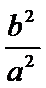
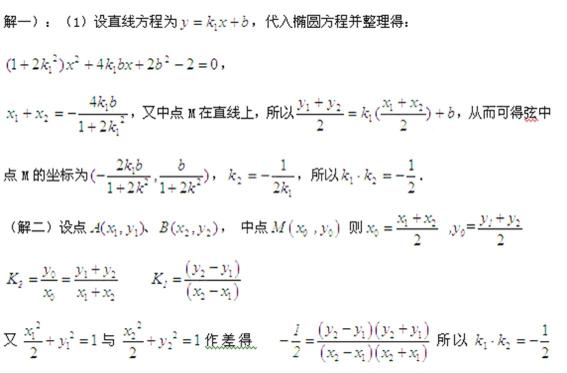
(解一)设直线方程为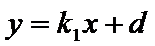
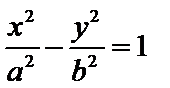
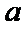
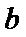
方程并整理得:
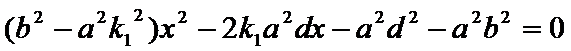
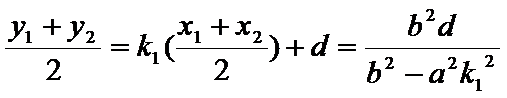
所以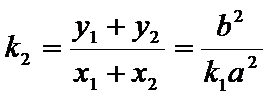
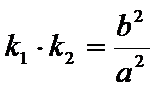
(解二)设点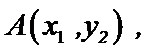
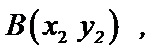
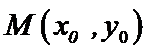
则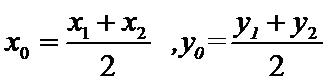
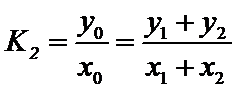
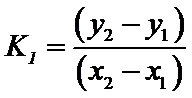
又因为点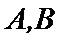
则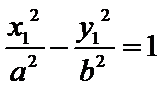
作差得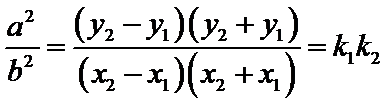
即
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
-243
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析