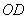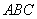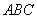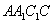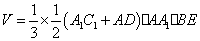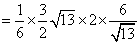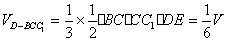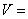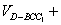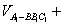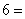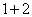- 平行关系的综合应用
- 共147题
在平面直角坐标系






正确答案
3/4
解析
略。
知识点
若直线



正确答案
解析
略
知识点
如图,直角梯形



(1)求证:
(2)求四面体
正确答案
见解析。
解析
(1)取BD的中点P,连接EP、FP,
∵△BCD中,PF为中位线,
∴PF∥DC且PF=
又∵AE∥CD,DC=2AE2
∴EA∥DC且EA=
由此可得PF∥EA,且PF=EA…(3分)
∴四边形AFPE是平行四边形,可得AF∥EP
∵EP⊂面BDE,AF⊄面BDE,∴AF∥面BDE
(2)∵BA⊥AC,面ABC⊥面ACDE,面ABC∩面ACDE=AC
∴BA⊥面ACDE,即BA就是四面体B﹣CDE的高,BA=2
∵DC=AC=2AE=2,AE∥CD
∴
因此,△CDE的面积为S△CDE=3﹣1=2…(12分)
∴四面体B﹣CDE的体积
知识点
给出下列四个命题:
① 命题

② 若0<a<1,则函数
③ 函数

④ 对于任意实数x,有


⑤ 若


其中真命题的序号是 (把所有真命题的序号都填上)。
正确答案
①③④
解析
略。
知识点
如图,直四棱柱











(1)求直四棱柱
(2)求证:

正确答案
见解析
解析
(1)底面直角梯形的面积
过







侧面积
(2)







知识点
如图,直三棱柱







(1)求直三棱柱
(2)求异面直线


正确答案
(1)
解析
(1)

∴
(2)取







连
在

知
在


在
∴
知识点
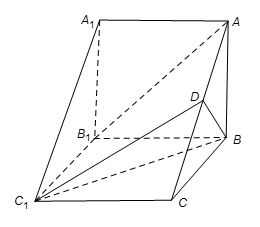
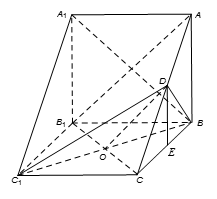
如图,在三棱柱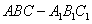
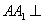
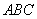
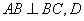
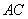
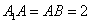
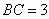
(1)求证: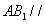
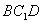
(2) 求四棱锥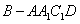
正确答案
见解析。
解析
(1)证明:连接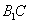
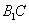
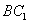
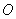
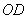
∵ 四边形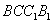
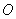
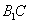
∵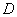
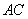
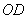
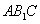
∴ 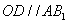
∵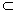

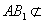
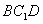
∴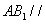
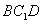
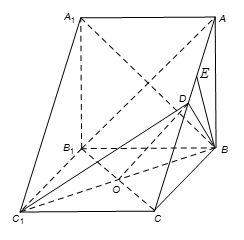
(2)解法1: ∵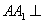
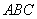
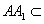
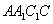
∴ 平面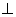
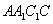
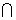
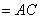
作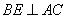
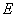
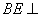
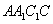
∵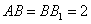
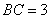
在Rt△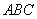
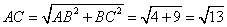
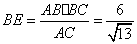
∴四棱锥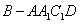
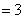
∴四棱锥
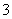
解法2: ∵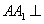
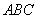
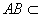
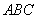
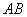
∵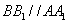

∵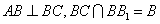
∴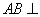
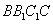
取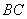
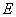
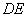
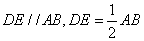
∴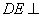
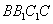
三棱柱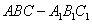
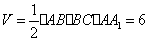
则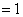
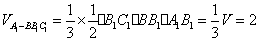
而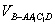
∴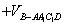
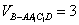
∴四棱锥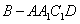
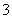
知识点
已知四棱锥



(1)求正视图的面积;
(2)求四棱锥
(3)求证:

正确答案
见解析。
解析
(1)
过A作
且
又∵

∴
∵



∴
正视图的面积为
(2)由(1)可知,四棱锥

底面积为
∴四棱锥
(3)证明:∵



∵在直角三角形ABE中,
在直角三角形ADC中,
∴

∴
又∵

知识点
如图,正方形





正确答案
解析
略
知识点
在正项等比数列


正确答案
解析
略
知识点
扫码查看完整答案与解析