- 平行关系的综合应用
- 共147题
如图,直四棱柱




(1)求证:

(2)求证:平面

正确答案
见解析
解析
(1)连接


由已知四边形


又



所以
因为



所以

(2)由已知
又



∴
∵


∵底面



∴
又



∴

∵
∴平面

知识点
已知双曲线与椭圆

正确答案
解析
略
知识点
四面体的四个面的面积分别为





正确答案
解析
略
知识点
定义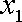
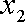
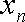
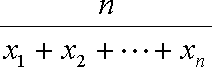
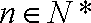
(1)若数列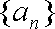
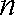
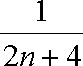
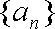
(2)设数列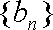
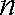
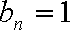
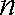
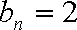
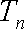
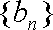
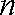
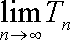
(3)设函数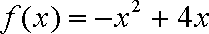
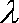

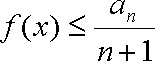
正确答案
见解析
解析
(1)设数列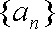
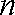
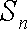
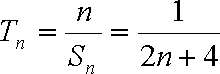
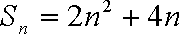
所以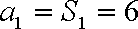

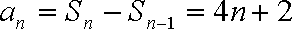
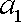
所以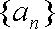
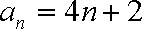
(2)设数列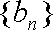
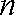
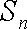
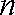
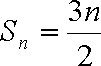
当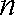
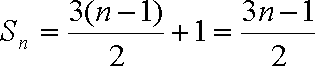
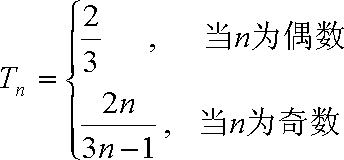
所以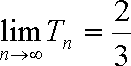
(3)假设存在实数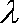

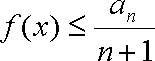
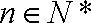
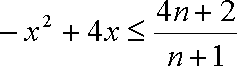
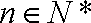
令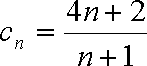
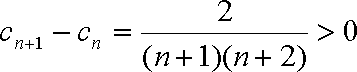
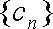
所以只要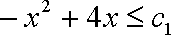
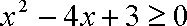


所以存在最大的实数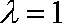

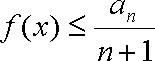
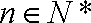
知识点
如图所示的几何体,是由棱长为2的正方体
(1)试画出该几何体的三视图;(主视图投影面平行平面
(2)若截面

正确答案
见解析
解析
(1) (每画对一个图形得2分)

(2)设原正方体中由顶点

结合题意,可知,



知识点
扫码查看完整答案与解析





















