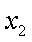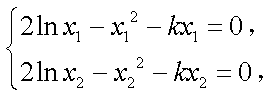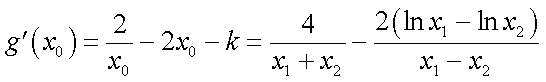- 平行关系的综合应用
- 共147题
如图,在三棱锥P—ABC中,平面PAC


求证:(1)
(2)平面DEF
正确答案
见解析。
解析
(1)在△PAC中,因为E,F分别是AP,
AC的中点,所以EF // PC。
又因为

所以
(2)连结CD,因为

因为F是AC的中点,所以
因为平面PAC 



所以
因为

知识点
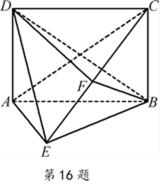
如图,在四棱锥E—ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1) AE∥平面BDF;
(2) 平面BDF⊥平面BCE。
正确答案
见解析
解析
证明(1) 设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以 在△ACE中,FG∥AE
因为 AE⊄平面BDF,FG⊂平面BDF,
所以 AE∥平面BDF。
(2) 因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE,
因为 AE⊂平面ABE,所以 BC⊥AE,
又AE⊥BE,BC∩BE=B,所以 AE⊥平面BCE,又FG∥AE,
所以FG⊥平面BCE,
因为 FG⊂平面BDF,所以平面BDF⊥平面BCE
知识点
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,

(1)求出该几何体的体积。
(2)若



(3)求证:平面

正确答案
见解析。
解析
(1)由题意可知:四棱锥
平面

所以,

又
则四棱锥

(2)连接
又






所以,

(3)


又平面


由(2)知:

又
所以,平面

知识点
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD, E、F、G、H分别是线段PA、PD、CD、BC的中点.
(1)求证:BC∥平面EFG;
(2)求证:DH⊥平面AEG;
(3)求三棱锥E-AFG与四棱锥P-ABCD的体积比.
正确答案
见解析。
解析
(1)∵BC∥AD,AD∥EF,∴BC∥EF,,,,,,,,,。2分

(2)∵PA⊥平面ABCD,∴PA⊥DH ,即 AE⊥DH,,,,,,,,,。5分
∵△ADG≌△DCH ,∴∠HDC=∠DAG,∠AGD+∠DAG=90°
∴∠AGD+∠HDC=90°
∴DH⊥AG
又∵AE∩AG=A,∴DH⊥平面AEG,,,,,,,,,,,。8分
(3)

知识点
设函数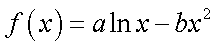
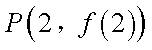
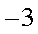
(1)求函数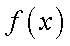
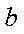
(2)当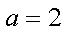
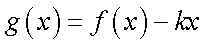
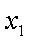
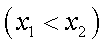
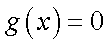
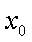
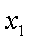
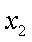
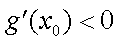
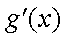
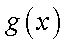
正确答案
见解析。
解析
(1)函数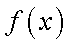
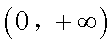
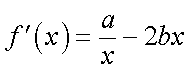
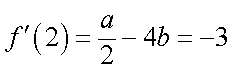
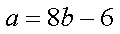
于是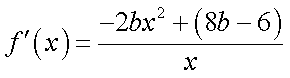
①当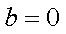
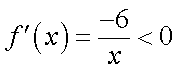
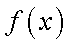
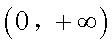
②当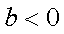
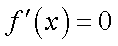
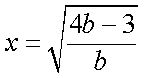
所以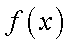
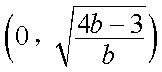
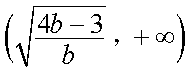
③当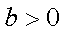
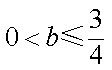
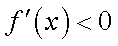
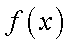
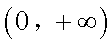
若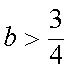
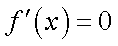
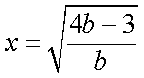
所以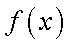
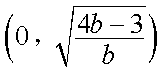
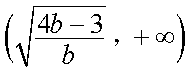
综上,若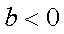
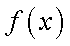
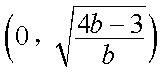
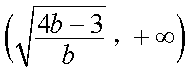
若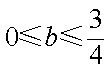
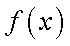
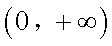
若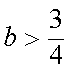
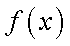
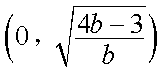
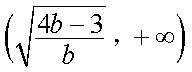
(2)因为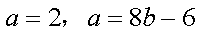
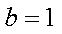
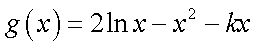
因为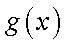
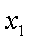
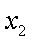
相减得: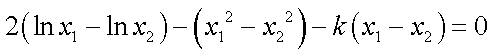
因为 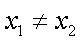
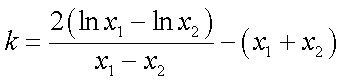
于是
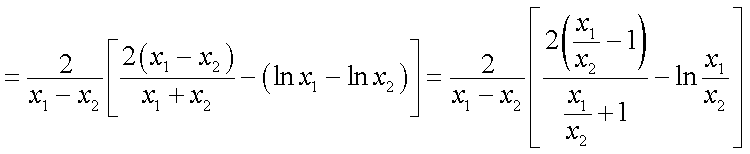
令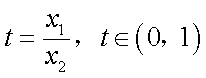
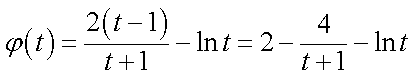
则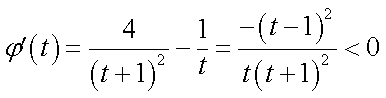
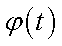
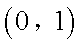
则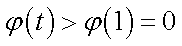
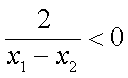
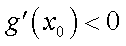
知识点
扫码查看完整答案与解析