- 函数的定义域及其求法
- 共105题
11.已知函数f(x)=Asin(2x+




正确答案
解析
考查方向
解题思路
根据三角函数的定义求出cosφ,得出φ;得出f(x)的解析式,利用正弦函数的单调性列出不等式解出
易错点
角
知识点
13.函数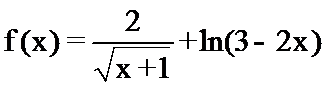
正确答案
解析
由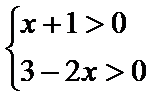
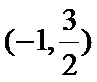
考查方向
解题思路
分别求出使得函数有意义的x的取值范围。
易错点
分母不可以为0忘记。
知识点
3.函数
正确答案
解析
由


考查方向
解题思路
本题考查对数函数的定义域与一元二次不等式式的解法,由对数的真数大于零得不等式求解.本题属于基础题.
易错点
注意不等式只能是大于零不能等于零
知识点
11.函数
正确答案
解析
由题意可得



考查方向
解题思路
1.根据函数有意义,得到不等式组;2.解题中给出的不等式组即可。
易错点
1.解不等式
知识点
2.函数
正确答案
解析


考查方向
基本函数与复合函数的定义.
解题思路
了解基本初等函数及其定义域以及基本初等函数与复合函数间的关系。
易错点
基本初等函数通过四则运算变成复合函数时定义域,求原各基本初等函数的定义域的交集。
教师点评
要求学生准确把握基本初等函数的定义域,熟悉复合函数的定义域是基本初等函数的定义域的交集。
知识点
已知函数

17.求函数的定义域
18.当 时,求 的最小值.
正确答案
解析


考查方向
解题思路
由被开方数的非负性,以及真数大于零的性质得到两个不等式,求公共部分得解.
易错点
熟悉简单分式不等式与一元二次不等式的解法
正确答案
解析

又

故
考查方向
解题思路
利用换元法求函数的单调性,利用单调性求最值。
易错点
熟悉换元法求最值的方法。
扫码查看完整答案与解析