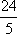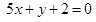- 函数的值域及其求法
- 共87题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
椭圆
A
B
C
D
正确答案
解析
因为A，B为左，右顶点，F1，F2为左，右焦点，
所以|AF1|＝a－c，|F1F2|＝2c，|F1B|＝a＋c.
又因为|AF1|，|F1F2|，|F1B|成等比数列，
所以(a－c)(a＋c)＝4c2，即a2＝5c2.
所以离心率
知识点
已知函数
正确答案
9。
解析
由值域为
∴
∴
∵不等式
知识点
若正数x，y满足x＋3y＝5xy，则3x＋4y的最小值是( )
A
B
C5
D6
正确答案
解析
∵x＋3y＝5xy，∴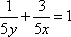
∴3x＋4y＝(3x＋4y)×1＝(3x＋4y)
＝
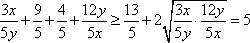
当且仅当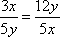
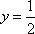
知识点
将函数y=sinx的图象向左平移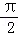
Ay=f（x）是奇函数
By=f（x）的周期为π
Cy=f（x）的图象关于直线x=
Dy=f（x）的图象关于点（﹣
正确答案
解析
将函数y=sinx的图象向左平移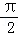
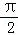
即f（x）=cosx。
∴f（x）是周期为2π的偶函数，选项A，B错误；
∵cos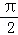
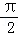
∴y=f（x）的图象关于点（﹣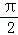
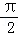
知识点
曲线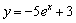
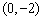
正确答案
解析
略
知识点
如图，在平面四边形ABCD中，DA⊥AB，DE＝1，
(1)求sin∠CED的值；
(2)求BE的长。
正确答案
见解析。
解析
如题图，设∠CED＝α.
(1)在△CDE中，由余弦定理，得EC2＝CD2＋DE2－2CD·DE·cos∠EDC.
于是由题设知，7＝CD2＋1＋CD，即CD2＋CD－6＝0.
解得CD＝2(CD＝－3舍去)。
在△CDE中，由正弦定理，得
于是，
即
(2)由题设知，
而
＝
在Rt△EAB中，
在第(1)问中，通过已知条件，借助余弦定理得到CD的长，然后在△CDE中，利用正弦定理得到∠CED的正弦值；在第(2)问中，利用∠CED的正弦值求得其余弦值，然后利用角之间的关系表示出∠AEB，进而表示出∠AEB的余弦值，最后在Rt△EAB中利用边角关系，求得BE的长。
知识点
函数
A
B
C
D
正确答案
解析
因为
知识点
若正实数X，Y 满足2X+Y+6=XY ， 则XY 的最小值是 。
正确答案
18
解析
运用基本不等式，
知识点
为了普及环保知识，增强环保意识，某大学随即抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为
A
B
C
D
正确答案
解析
计算可以得知，中位数为5.5，众数为5所以选D
知识点
扫码查看完整答案与解析