· 函数概念与表示

· 函数的定义域及其求法

函数的定义域及其求法
共105题

· 函数概念与表示

· 函数的定义域及其求法

函数的定义域及其求法
共105题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 14 分

已知函数，函数是函数的反函数。

（1）求函数的解析式，并写出定义域；

（2）设函数，试判断函数在区间上的单调性，并说明你的理由。

正确答案

（1）（2）函数在上单调递减

解析

（1），

.又，.

.

由，可解得.

，

（2）答：函数在区间上单调递减.

理由：由（1）可知，.

可求得函数的定义域为.

对任意，有，

所以，函数是奇函数.

当时，在上单调递减，在上单调递减，

于是，在上单调递减.

因此，函数在上单调递减.

依据奇函数的性质，可知，函数在上单调递减.

知识点

函数的定义域及其求法函数单调性的判断与证明反函数

1

题型：单选题

|

单选题 · 5 分

若函数的定义域为M={-2，0，2}，值域为N，则M∩N=

A{-2，0，2}

B{0，2}

C{2}

D{0}

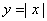
正确答案

B

解析

略

知识点

并集及其运算函数的定义域及其求法函数的值域及其求法

1

题型：单选题

|

单选题 · 5 分

函数的定义域为（）

A

B

C

D

正确答案

A

解析

知识点

函数的定义域及其求法

1

题型：单选题

|

单选题 · 5 分

函数的定义域是

A

B

C

D

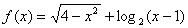
正确答案

A

解析

略

知识点

函数的定义域及其求法

1

题型：单选题

|

单选题 · 5 分

设函数的定义域为，则

A

B

C

D

正确答案

D

解析

略

知识点

补集及其运算函数的定义域及其求法

继续学习学习下一知识点

下一知识点 : 函数的值域及其求法

百度题库 > 高考 > 文科数学 > 函数的定义域及其求法

扫码查看完整答案与解析