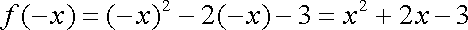- 函数的定义域及其求法
- 共105题
对于实数







①

(1)若

(2)当



正确答案
(1)
(2)
解析
(1)若


(2)当





①当



②当



综上,
知识点
已知二次函数f(x)满足条件f(0)=1,f(x+1)-f(x)=2x.
(1)求f(x);
(2)求f(x)在区间[-1,1]上的最大值和最小值。
正确答案
见解析。
解析
(1)设函数f(x)=ax2+bx+c(a≠0)
∵f(0)=1, ∴c=1;……………………………1分
∵f(x+1)-f(x)=2x
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x…………………………3分
即:2ax+a+b=2x
∴
∴
(2)f(x)=x2-x+1
ymin=f(

知识点
已知
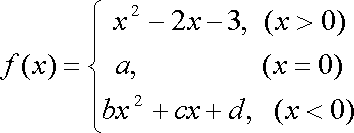
(1)分别求
(2)画出
正确答案
见解析。
解析
y=f(x)是定义在R上的奇函数,则f(0)=0, 得: a=0,
设x<0时,则-x>0,
而f(x)为R上的奇函数,所以f(-x)=-f(x)
所以当x<0时,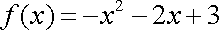
故b= -1, c= -2, d=3.---------------6分
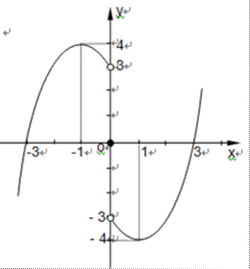
(2) 简图如下------------10分
由图象可得: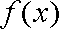
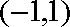
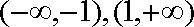
知识点
集合A是由具备下列性质的函数
(a)函数

(b)函数

(c)函数

(1)判断函数

并简要说明理由;
(2)对于(1)中你认为属于集合A的函数


正确答案
见解析。
解析
(1)函数
因为


因为:a函数


c函数

(2)



知识点
如果函数







正确答案
解析
“三角形函数”的函数值都为正数,且最小值的2倍大于最大值. ①















知识点
扫码查看完整答案与解析