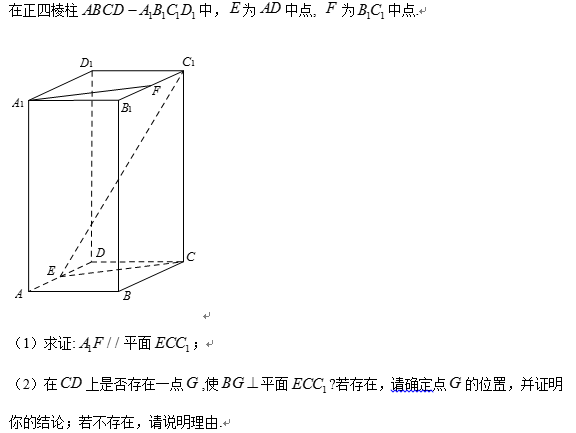
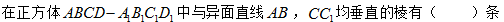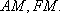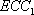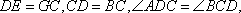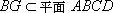- 平面与平面平行的判定与性质
- 共156题
已知四棱锥


正确答案
解析
可证四个面都是直角三角形,其面积
知识点
正确答案
解析
略
知识点
正确答案
见解析
解析
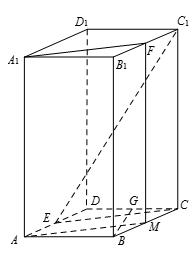
(1)证明:在正四棱柱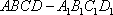
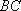
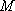
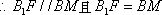

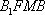
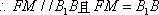
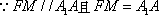

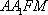
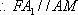
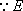
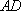
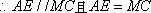

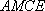
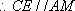
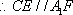
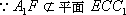
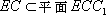
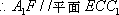
(2) 证明:在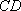
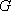
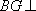
取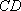
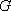
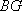
在正方形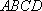
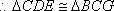
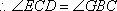
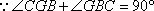
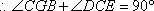
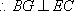
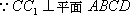
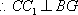
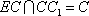
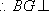
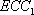
故在CD上存在中点G,使得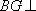
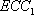
知识点
三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=BC=AC=AA1,CD⊥AC1,E、F分别是BB1、CC1中点。
(1)证明:平面DEF∥平面ABC;
(2)证明:CD⊥平面AEC1。
正确答案
见解析
解析
(1)证明:由题意可知CA=CC1,又CD⊥AC1,
由等腰三角形的性质可知D为AC1的中点,
又F为CC1的中点,所以DF∥AC,
又AC⊂平面ABC,所以DF∥平面ABC,
同理可证:EF∥平面ABC,又DF∩EF=F,
所以平面DEF∥平面ABC;
(2)设AB=2,则DF=1,EF=2,∠DFE=∠ACB=60°,
由余弦定理可得:DE2=12+22

∵CD为直角三角形ACC1斜边AC1的中线,
∴CD=


所以CD2+DE2=CE2,由勾股定理可得CD⊥DE,
又CD⊥AC1,AC1∩DE=D,所以CD⊥平面AEC1,
知识点
如图,在四棱锥
(1)若点E为棱PA上一点,且OE∥平面PBC,求
(2)求证:平面PBC⊥平面PDC.
正确答案
解析
(1)因为OE∥平面PBC,OE平面PAC,平面PAC∩平面PBC=PC,所以OE∥PC,
所以AO∶OC=AE∶EP,
因为DC//AB,DC=2AB,所以AO∶OC=AB∶DC=1∶2.
所以
(2)法一:取PC的中点F,连结FB,FD。
因为△PAD是正三角形,DA=DC,所以DP=DC。
因为F为PC的中点,所以DF⊥PC.
因为AB平面PAD,所以AB⊥PA,AB⊥AD,AB⊥PD。
因为DC//AB,所以DC⊥DP,DC⊥DA。
设AB=a,在等腰直角三角形PCD中,DF=PF=a。
在Rt△PAB中,PB=a。
在直角梯形ABCD中,BD=BC=a。
因为BC=PB=a,点F为PC的中点,所以PC⊥FB。
在Rt△PFB中,FB=a,
在△FDB中,由DF=a,FB=a,BD=a,可知DF2+FB2=BD2,所以FB⊥DF。
由DF⊥PC,DF⊥FB,PC∩FB=F,PC、FB平面PBC,所以DF⊥平面PBC。
又DF平面PCD,所以平面PBC平面PDC,
法二:取PD,PC的中点,分别为M,F,连结AM,FB,MF,
所以MF∥DC,MF=DC。
因为DC//AB,AB=DC,所以MF∥AB,MF=AB,
即四边形ABFM为平行四边形,所以AM∥BF,
在正三角形PAD中,M为PD中点,所以AM⊥PD。
因为AB⊥平面PAD,所以AB⊥AM。
又因为DC//AB,所以DC⊥AM。
因为BF//AM,所以BF⊥PD,BF⊥CD。
又因为PD∩DC=D,PD、DC平面PCD,所以BF⊥平面PCD。
因为BF平面PBC,所以平面PBC平面PDC.
知识点
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点。
(1)求证:DE∥平面PBC;
(2)求三棱锥A-PBC的体积。
正确答案
见解析。
解析
(1)
如图,取AB的中点F,连接DF,EF。
在直角梯形ABCD中,CD∥AB,且AB=4,CD=2,所以
所以四边形BCDF为平行四边形,所以DF∥BC,(2分)
在△PAB中,PA=EA,AF=FB,所以EF//PB。
又因为DF

所以平面DEF∥平面PBC. (4分)
因为DE
(2)取AD的中点O,连接PO。
在△PAD中,PA=PD=AD=2,所以PO⊥AD,
又因为平面PAD⊥平面ABCD,平面PAD
所以PO⊥平面ABCD。
直角梯形ABCD中,CD//AB,且AB=4,AD=2,AB⊥AD,
所以
故三棱锥A-PBC的体积
知识点
已知

(1)若


(2)若

(3)设函数





正确答案
见解析。
解析

(1)因为


所以

所以



所以
(2)因为

所以
所以

因为



而



所以
由


因为


令

当


当


所以当



所以

(3)因为


所以


所以
所以
其对称轴为



所以在


知识点
已知四棱锥
(1)求此四棱锥的体积;
(2)若E是PD的中点,求证:
(3) 在(2)的条件下,若F是
正确答案
见解析。
解析
(1)由题意可知,四棱锥


(2)由三视图可知,

∵
又



∴

∵

又
又



∴

(3)∵


又∵


∴四边形



所以,直线AE和直线BF既不平行也不异面。
知识点
已知向量 
(1)若

(2)若函数

正确答案
见解析。
解析
知识点
如图,经过村庄






正确答案
见解析。
解析
设∠AMN=θ,在△AMN中,
因为MN=2,所以
在△APM中,cos∠AMP=cos(60°+θ)。
AP2=AM2+MP2-2 AM·MP·cos∠AMP
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值2。
答:设计∠AMN为60度时,工厂产生的噪声对居民的影响最小,
解法二(构造直角三角形):
设∠PMD=θ,在△PMD中,
∵PM=2,∴PD=2sinθ,MD=2cosθ。
在△AMN中,∠ANM=∠PMD=θ,
当且仅当


此时AM=AN=2,∠PAB=30°
解法三:设AM=x,AN=y,∠AMN=α。
在△AMN中,因为MN=2,∠MAN=60°,
所以MN2=AM2+AN2-2 AM·AN·cos∠MAN,
即x2+y2-2xycos60°=x2+y2-xy=4。
因为

在△AMP中,AP2=AM2+PM2-2 AM·PM·cos∠AMP,
即AP2=x2+4-2×2×x×
因为x2+y2-xy=4,4+xy=x2+y2≥2xy,即xy≤4。
所以AP2≤12,即AP≤
当且仅当x=y=2时,AP取得最大值
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小,
解法四(坐标法):以AB所在的直线为x轴,A为坐标原点,建立直角坐标系。
设M(x1,0),N(x2,x2),P(x0,y0),∵MN=2,
∴(x1-x2)2+3x22=4。
MN的中点
∵△MNP为正三角形,且MN=2,∴PK=
kMN·kPK=-1,即 
∴y0-x2=(x0-),∴

答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小,
解法五(变换法):
以AB所在的直线为x轴,A为坐标原点,建立直角坐标系。
设M(x1,0),N(x2,
∵MN=2,∴(x1-x2)2+3x22=4,即x21+4x22=4+2x1x2
∴4+2x1x2≥4x1x2,即x1x2≤2。
∵△MNP为正三角形,且MN=2,∴PK=





=4+4x1x2≤4+4×2=12
即AP≤
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小,
解法六(几何法):
由运动的相对性,可使△PMN不动,点A在运动。
由于∠MAN=60°,∴点A在以MN为弦的一段圆弧(优弧)上,
设圆弧所在的圆的圆心为F,半径为R,
由图形的几何性质知:AP的最大值为PF+R。
在△AMN中,由正弦定理知:
∴R=
∴FM=FN=R=
设PF与MN交于E,则FE2=FM2-ME2=R2-12=
答:设计AM=AN=2 km时,工厂产生的噪声对居民的影响最小。
知识点
扫码查看完整答案与解析