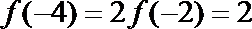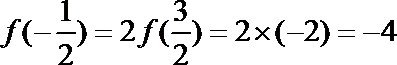- 函数的图象
- 共14题
9.已知函数y = f (x) 和 y = g (x) 的定义域及值域均为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在 R 上的函数 f (x)满足 f (x + 2) = 


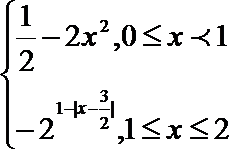
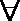
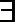
正确答案
解析
∵当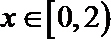

∴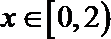

∵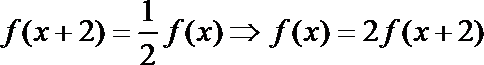
∵当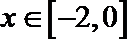
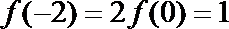
∵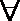
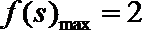
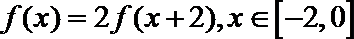
∵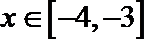

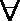
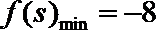
∵函数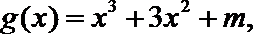
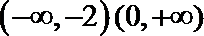
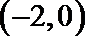
∴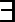

考查方向
本题主要考查函数与不等式综合应用
解题思路
由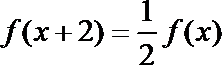
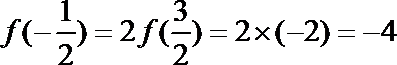
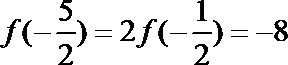
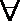
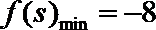
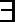
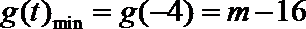
易错点
分段函数如何转化求出最值
知识点
14. 某食品的保鲜时间t(单位:小时)与储藏温度x(单位:


已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示. 给出以下四个结论:
①该食品在
②当
③到了此日13时,甲所购买的食品还在保鲜时间内;
④到了此日14时,甲所购买的食品已然过了保鲜时间.
其中,所有正确结论的序号是____.
正确答案
①④
解析
因为某食品的保鲜时间t(单位:小时)与储藏温度x(单位:











考查方向
解题思路
因为某食品的保鲜时间t(单位:小时)与储藏温度x(单位:











易错点
本题易在判定在

知识点
12.已知函数



正确答案
1
解析
由上面思路可知


考查方向
解题思路
由函数的图像可知:当0



易错点
不能顺利把不等式问题转化为图像的平移问题,而过份依赖由具体不等式才能解题,对于抽象函数无能为力的思维局限而无法作答出错。
知识点
扫码查看完整答案与解析