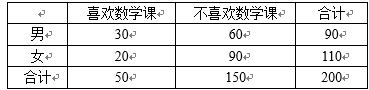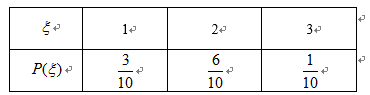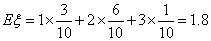- 独立性检验的基本思想
- 共2题
某种机器在一个工作班的8小时内,需要工作人员操控累计2个小时才能正常进行,当机器需用操控而无人操控时,机器自动暂停运行。每台机器在某一时刻是否用人操控彼此之间相互独立
21.若在一个工作班内有4台相同机器,求在同一时刻需用人操控的平均台数;
22.若要求一人操控的所有机器正常运行的概率控制在不低于




正确答案
(1)
解析
试题分析:本题属于概率问题,属于基础题,意在考查考生对基本概念的理解。
(Ⅰ)用




考查方向
解题思路
(1)用二项分布求数学期望
(2)首先要理解n取1,2,3时是属于什么概率问题,根据情况求出工作人员待工而闲的概率。
易错点
审题不清,不会用数学知识来转化。
正确答案
(2)一个工作人员操控2台机器符合要求
解析
试题分析:本题属于概率问题,属于基础题,意在考查考生对基本概念的理解。
(Ⅱ)设

①当

此时,一人操控1台机器,工作人员能够及时操控机器,不会出现机器等待操控的情形,但工作人员待工而闲的概率为
②当



此时,一人操控2台机器,在同一时刻需要操控2台机器的概率为



③当



此时,一人操控3台机器,出现机器等待工作人员操控而不能正常运行的概率为


综上所述,一个工作人员操控2台机器符合要求.
考查方向
解题思路
(1)用二项分布求数学期望
(2)首先要理解n取1,2,3时是属于什么概率问题,根据情况求出工作人员待工而闲的概率。
易错点
审题不清,不会用数学知识来转化。
为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下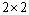
(1)根据独立性检验的基本思想,约有多大的把握认为“性别与喜欢数学课之间有关系”?
(2)若采用分层抽样的方法从不喜欢数学课的学生中随机抽取5人,则男生和女生抽取的人数分别是多少?
(3)从(2)随机抽取的5人中再随机抽取3人,该3人中女生的人数记为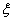
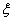
正确答案
见解析。
解析
(1)∵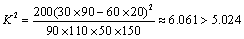
∴约有97.5%以上的把握认为“性别与喜欢数学课之间有关系”.
(2)男生抽取的人数有: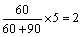
女生抽取的人数各有: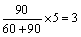
(3)由(2)可知,男生抽取的人数为2人,女生抽取的人数为3人,
所以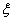
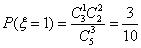
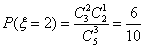
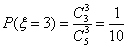
所以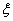
所以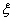
知识点
扫码查看完整答案与解析