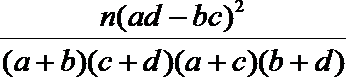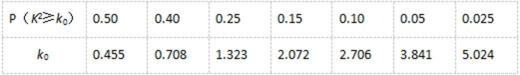- 独立性检验的应用
- 共11题
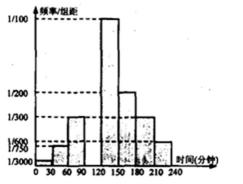
20.某校高一年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查。根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,l50),[150,180),[180,210),[210,240),得到频率分布直方图如下图。已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人。
(1)求n的值并求有效学习时间在[90,120)内的频率;
(2)如果把“学生晚上有效时间达到两小时”作为是
否充分利用时间的标准,对抽取的n名学生,请
补完整下列2×2列联表并判断是否有95%的把握
认为学生利用时间是否充分与走读、住宿有关?
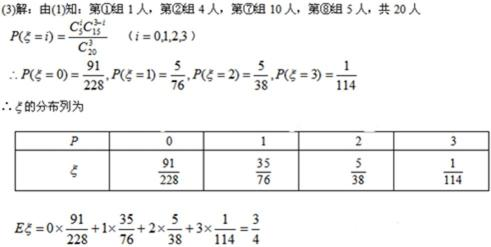
(3)若在第①组、第②组、第⑦组、第⑧组中共抽出3
人调查影响有效利用时间的原因,记抽到“有效学
习时间少于60分钟”的学生人数为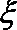
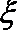
参考公式:K2=
参考列表:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.为了考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校的高中生中随机地抽取了300名学生进行调查,得到如下列联表:
由表中数据计算
正确答案
可以有95%的把握认为“高中生的性别与是否喜欢数学课程之间有关系”,作出这种判断的依据是独立性检验的基本思想,具体过程为:
分别用a,b,c,d表示喜欢数学的男生数、不喜欢数学的男生数、喜欢数学的女生数、不喜欢数学的女生数
如果性别与是否喜欢数学有关系,则男生中喜欢数学的比例

即
将上式等号右边的式子乘以常数因子
然后平方计算得:
因此,
另一方面,假设“性别与是否喜欢数学课程之间没有关系”
由于事件


而由样本计算得
由此我们可以断定“性别与是否喜欢数学之间有关系”成立
并且这种判断出错的可能性为5%
约有95%的把握认为“性别与是否喜欢数学课程之间有关系”
解析
解析已在路上飞奔,马上就到!
知识点
5.某人研究中学生的性别与阅读量的关系,随机抽查500名中学生,得到统计数据如下表:
附表:
参照附表,可得到的结论是( ).
正确答案
解析
由K2=

知识点
为了调查我市在校中学生参加体育运动的情况, 从中随机抽取了16名男同学和14名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率, 从我市中学生中随机抽取3人,若其中喜爱运动的人数为

正确答案
见解析。
解析
(1)
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关
(3)统计结果中喜爱运动的中学生所占的频率为
喜爱运动的人数为


喜爱运动的人数为
因为


知识点
19. 有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
参考公式:
参考数据:
正确答案
解:(1)
(2)根据列联表中的数据,得到 
因此有95%的把握认为“成绩与班级有关系”.
(3)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y).
所有的基本事件有(1,1)、(1,2)、(1,3)、……、(6,6),共36个.
事件A包含的基本事件有:
(1,5)、(2,4)、(3,3)、(4,2)、
(5,1)(4,6)、(5,5)、(6、4),共8个

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析